Cho hai chữ số a và 8. Biết tổng hai chữ số lậ được từ các chữ số đã cho là 143. Tím tích hai số đó . Nhờ các bạn giúp đơ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 9 2019
ez
a:b có thể là 1 số tự nhiên bất kì nên a,b 
vậy có
hm.......................................................................................................................................khó khăn đây
có vô số
30 tháng 9 2018
Gọi số cần tìm là a7. Theo đề bài ta có:
a7 : (a + 7) = 5 dư 12
a x 10 + 7 = 5 x (a + 7) + 12
a x 10 + 7 = 5 x a + 35 + 12
a x 5 = 40
a = 40 : 5 = 8
Vậy số cần tìm là 87.
Đáp số: 87
CM
9 tháng 4 2019
Giả sử a là chữ số hàng chục và b là chữ số hàng đơn vị của số cần tìm
Ta có:
Tập hợp A:
Số cần tìm là số có hai chữ số nên chữ số hàng chục a ≠ 0.
Vì a + b = 8 nên a chỉ có thể lấy các giá trị 1, 2, 3, 4, 5, 6, 7, 8.
Vậy, Tập hợp A = {17 ; 26 ; 35 ; 44 ; 53 ; 62 ; 71 ; 80}.
Tập hợp B:
Số cần tìm là số có hai chữ số nên chữ số hàng chục a ≠ 0.
Số cần tìm được tạo thành từ hai trong bốn số 0 ; 3 ; 5 ; 8
Vậy, Tập hợp B = {30 ; 35 ; 38 ; 50 ; 53 ; 58 ; 80 ; 83 ; 85}.
26 tháng 11 2021
Gọi số đó là ab
Theo đề ta có:
ab + ba = 143
Suy ra 10( a+b ) + a + b = 143 => 11 ( a + b ) = 143
=> a + b = 13 ; b - a = 3
=> a = 5; b = 8
Vậy số đó là 58
CM
28 tháng 5 2019
Gọi a là chữ số hàng chục, b là chữ số hàng đơn vị. Điều kiện a, b nguyên 1 ≤ a ≤ 9 và 0 ≤ b ≤ 9. Ta có:
'
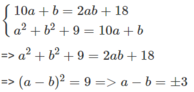Trường hợp 1
a - b = 3 ⇒ a = b + 3
Thay vào phương trình đầu của hệ phương trình ta được:
11b + 30 = 2(b + 3)b + 18 ⇒ 2 b 2 - 5 b + 12 = 0
Phương trình cuối có hai nghiệm: b 1 = 4 , b 2 = -3/2
Giá trị b 2 = -3/2 không thỏa mãn điều kiện 0 ≤ b ≤ 9 nên nên bị loại.
Vậy b = 4, suy ra a = 7.
Trường hợp 2
a - b = - 3 ⇒ a = b - 3
Thay vào phương trình của hệ phương trình ra được
11b - 30 = 2(b - 3)b + 18 ⇒ 2 b 2 - 17 b + 48 = 0
Phương trình này vô nghiệm.
Vậy số phải tìm là 74.
Xét a là các chữ số từ 0 đến 9 ta thấy: 2 số lập được từ a và 8 có tổng là 143 chỉ thỏa mãn khi a = 5. Ta lập được 2 số 85 và 58
Tích của 85 và 58 là: \(85\times58=4930\)
Còn nếu hỏi theo hướng tích của 5 và 8 thì kết quả là: \(5\times8=40\)