Đề bài: Giả định có một hộp kem đánh răng có kích thước như sau: Chiều dài: 22cm, Chiều rộng: 5cm, Chiều cao: 4cm.
Yêu cầu: Hãy tính kích thước của một hộp to với chi phí thấp nhất để hộp to đó có thể đựng được 60 hộp kem đánh răng nhỏ với kích thước như trên.
Lưu ý: Hộp to là chất liệu Carton 3 lớp và có độ dày là 5mm.



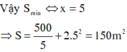

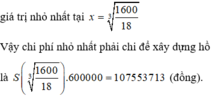

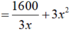

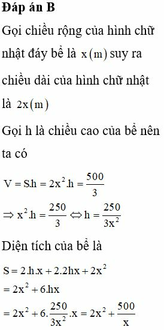


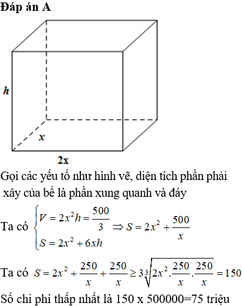



Tổng thể tích 60 hộp kem là
60.22.5.4=26400 cm3
Hộp to phải là hộp có thể tích = 26400 cm3
Gọi kích thước của hộp to lần lượt là x; y; z
Thể tích hộp là: V= x.y.z=26400
Diện tích toàn phần của hộp to là: 2.(xy+yz+xz)
Chi phí thấp nhất khi diện tích toàn phần của hộp to nhỏ nhất
=> xy+yz+zx nhỏ nhất
Áp dụng BĐT Cauchy
\(xy+yz+xz\ge3\sqrt[3]{xy.yz.xz}=3\sqrt[3]{V^2}\)
Dấu = xảy ra khi xy=yz=xz => x=y=z
\(\Rightarrow x=y=z=\sqrt[3]{26400}\) => hộp to có dạng hình lập phương