LCM(3;4;10)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



LCM ?
Tớ nhớ lớp 6 đâu có cái này
ước chung hay ước chung lớn nhất phải không
\(ưc\)( 7 ; 14 ) = 1 ; 7
\(ưcln\)( 7 ; 14 ) = 7

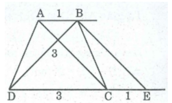
Phân tích: Giả sử hình thang ABCD dựng được thỏa mãn điều kiện bài toán
Từ B kẻ đường thẳng song song với AC cắt CD tại E. Tứ giác ABEC là hình thang có hai cạnh bên song song nên CE = AB = l cm, BE = AC = 3cm
Tam giác BDE xác định được, ta cần xác định đỉnh C và A.
- Đỉnh C nằm trên tia DE cách D một khoảng bằng 3cm
- Đỉnh A nằm trên đường thẳng đi qua B và song song với CD, A cách C một khoảng bằng 3 cm. (ABCD là hình thang cân nên AC = BD = 3 cm)
Cách dựng:
- Dựng ∆ BDE biết BD = 3cm, BE = 3cm , DE = 4cm
- Dựng điểm C trên tia DE sao cho DC = 3cm
- Dựng đường thẳng d đi qua B song song với CD.
- Dựng cung tròn tâm C bán kính 3 cm cắt đường thắng d tại A. Nối AD ta có hình thang ABCD dựng được.
Chứng minh: Thật vậy theo cách dựng ta có AB // CD.
Tứ giác ABCD là hình thang. CD = 3cm, AC = BD = 3cm. Vậy ABCD là hình thang cân thỏa mãn điều kiện bài toán.
Bài toán có một nghiệm hình.

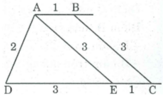
Phân tích:
Giả sử hình thang ABCD dựng được thỏa mãn điều kiện bài toán.
Qua A kẻ đường thẳng song song với BC cắt CD tại E ta thấy tam giác AED xác định vì biết ba cạnh, ta cần xác định đình B và C.
- Đỉnh C nằm trên tia DE, cách D một khoảng bằng 4cm.
- Đỉnh B nằm trên đường thẳng đi qua A song song với đường thẳng DE và cách A một khoảng bằng lcm.
Cách dựng:
- Dựng ∆ ADE biết AD = 2cm, DE = 3cm, AE = 3cm
- Trên tia DE dựng điểm C sao cho DC = 4cm
- Dựng đường thẳng đi qua A và song song với DC, lấy điểm B sao cho AB = lcm. Nối BC ta có hình thang ABCD cần dựng.
Chứng minh:
Thật vậy, theo cách dựng ta có AB // CD nên tứ giác ABCD là hình thang.
Ta có: AD = 2cm, DC = 4cm, AB= lcm, hình thang ABCE có hai cạnh đáy AB = EC = 1cm nên BC = AE = 3cm.
Hình thang ABCD thỏa mãn điều kiện bài toán.
Biện luận: Tam giác ADB luôn dựng được nên hình thang ABCD dựng được, bài toán có một nghiệm hình.

1. Độ tụ của kính phải đeo:
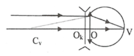
a) Kính đeo sát mắt:
Để nhìn thấy vật ở vô cực mà mắt không điều tiết thì:
Vật ở vô cực qua kính đeo cho ảnh phải hiện lên ở điểm cực viễn của mắt nên tiêu cự ca kính phải đeo là
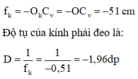
b) Kính cách mắt 1cm:
Để nhìn thấy vật ở vô cực mà mắt không điều tiết thì:
Vật ở vô cực qua kính đeo cho ảnh phải hiện lên ở điểm cực viễn của mắt nên tiêu cự của kính phải đeo là
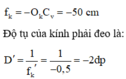
c) Điểm gần nhất mà mắt đeo kính nhìn thấy:
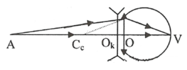
+ Kính đeo sát mắt:
Điểm A gần nhất mà mắt đeo kính thấy được có vị trí xác định bởi:
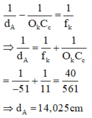
Điểm A cách mắt một đoạn 14,025 cm.
+ Kính cách mắt 1cm:
Điểm B gần nhất mà mắt đeo kính thấy được có vị trí xác định bởi:
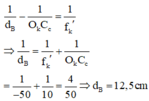
Điểm B cách mắt một đoạn 13,5cm.
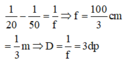
3. Để đọc sách trên mà chỉ có kính hội tụ có tiêu cự f = 28,8 cm thì kính phải đặt cách mắt một đoạn 1, ta có:

Vậy để đọc sách trên mà chỉ có kính hội tụ có tiêu cự f = 28,8 cm thì kính phải đặt cách mắt một đoạn l = 3 cm

Ta đặt: OA = d; OA’ = d’; OF = OF’ = f
+) Vật AB cách thấu kính d = 36 cm, vật ngoài khoảng OF.
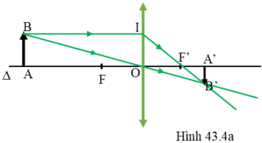
Trên hình 43.4a, xét hai cặp tam giác đồng dạng:
ΔABO và ΔA’B’O; ΔA’B’F’ và ΔOIF’.
Từ hệ thức đồng dạng được:
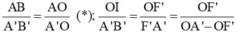
Vì AB = OI (tứ giác BIOA là hình chữ nhật)
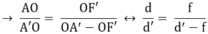
↔ dd’ – df = d’f (1)
Chia cả hai vế của (1) cho tích d.d’.f ta được:
![]()
(đây được gọi là công thức thấu kính cho trường hợp ảnh thật)
Thay d = 36cm, f = 12cm ta tính được: OA’ = d’ = 18cm
Thay vào (*) ta được:
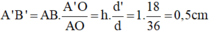
+) Vật AB cách thấu kính d = 8 cm, vật nằm trong khoảng OF
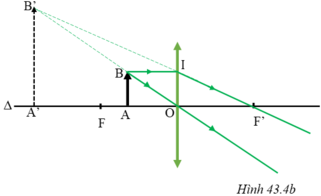
Trên hình 43.4b, xét hai cặp tam giác đồng dạng:
ΔA’B’F’ và ΔOIF’; ΔOAB và ΔOA’B’.
Từ hệ thức đồng dạng ta có:
![]()
Vì AB = OI (tứ giác BIOA là hình chữ nhật)
![]()
↔ dd’ + df = d’f (2)
Chia cả hai vế của (2) cho tích d.d’.f ta được:
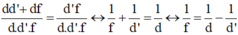
(đây được gọi là công thức thấu kính cho trường hợp ảnh ảo)
Thay d = 8cm, f = 12cm ta tính được: OA’ = d’ = 24cm
Thay vào (**) ta được:
![]()
LCM(3,4,10)=60\ NH
KB NHA
THANK NHIU NHIU