Tìm X : x15 = x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x^{15}=x.1\)
\(\Rightarrow x^{15}=x\)
\(TH1\)
\(x=0\)
\(\Rightarrow0^{15}=0\)
\(\Rightarrow1=0\)(Vô lí)
\(TH2\)
\(x\ge2\)
\(Cho\) \(x=2\)
\(\Rightarrow2^{15}=2\)(Vô lí)
\(TH3\)
\(x=1\)
\(\Rightarrow1^{15}=1\)
\(\Rightarrow1=1\)(t/m)
Vậy x=1
x¹⁵ = x.1
x¹⁵ = x
x¹⁵ - x = 0
x.(x¹⁴ - 1) = 0
x = 0 (nhận) hoặc x¹⁴ - 1 = 0
*) x¹⁴ - 1 = 0
x¹⁴ = 0 + 1
x¹⁴ = 1
x = 1 (nhận) hoặc x = -1 (loại)
Vậy x = 0; x = 1

\(x^{15}=x\\\Rightarrow x^{15}-x=0\\\Rightarrow x(x^{14}-1)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x^{14}-1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x^{14}=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)
Vậy: \(x\in\left\{0;1;-1\right\}\)
x¹⁵ = x
x¹⁵ - x = 0
x.(x¹⁴ - 1) = 0
x = 0 hoặc x¹⁴ - 1 = 0
*) x¹⁴ - 1 = 0
x¹⁴ = 1
x = 1 hoặc x = -1
Vậy x = 0; x = -1; x = 1

Bài 1.
\(x\times15+x\times35=250\)
\(x\times\left(15+35\right)=250\)
\(x\times50=250\)
\(x=250:50\)
\(x=5\)
\(------\)
\(718-x\times5=173\)
\(x\times5=718-173\)
\(x\times5=545\)
\(x=545:5\)
\(x=109\)

a ) x − 1 2 = 7 13 . 13 28 ; x − 1 2 = 1 4 b ) x 15 = − 3 11 . 77 36 ; x 15 = − 7 12 ; x = 15. − 7 12 c ) x + 7 7 = 9 18 . 9 27 ; x + 1 = 1 6 d ) x : 15 11 = − 3 12 .8 ; x : 15 11 = − 2 ; x = ( − 2 ) . 15 11

x15+32x+x1=780
xxx+(15+320+1)=780
xxx+336 =780
xxx = 780-336
xxx = 444
<=>x.(15+32+1)=780
<=>x.48 =780
<=>x =780:48
<=>x =16,25
Vậy x=15,25

a, 2 x . 4 = 128
=> 2 x = 128 : 4
=> 2 x = 32
=> 2 x = 2 5
=> x = 5
Vậy x = 5
b, x 15 = x
=> x = 1 hoặc x = 0
Vì 1 15 = 1 ; 0 15 = 0
c, x - 5 4 = x - 5 6
=> x – 5 = 1 hoặc x – 5 = 0
=> x = 6 hoặc x = 5
Vậy x = 6 hoặc x = 5
d, x 2018 = x 2
=> x = 1 hoặc x = 0
Vì 1 2018 = 1 2 = 1 ; 0 2018 = 0 2 = 0

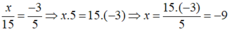
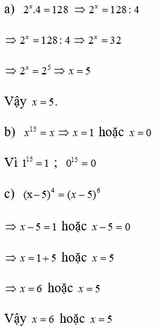
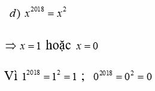
\(x^{15}-x=0\Leftrightarrow x\left(x^{14}-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x^{14}=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)
`x^{15}=x`
`x^{15}-x=0`
`x.(x^{14}-1)=0`
`@TH1: x=0`
`@TH2:x^{14}-1=0`
`=>x^{14}=1`
`=>x^{14}=1^{14}` hoặc `x^{14}=(-1)^{14}`
`=>x=1` hoặc `x=-1`
Vậy \(x \in {{0;1;-1}}\)