công thức tính số tự nhiên n của một dãy số
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
V
1
9 tháng 9 2021
Có thể biểu diễn dãy số tự nhiên trên tia số: Số 0 ứng với điểm gốc của tia số. Mỗi số tự nhiên ứng với một điểm trên tia số.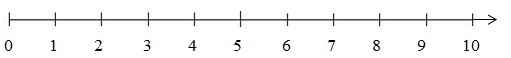
AH
Akai Haruma
Giáo viên
25 tháng 6 2024
Lời giải:
a. Quy luật: Các số của dãy, kể từ số thứ hai, bằng số liền trước của nó nhân với hai.
Vậy tổng 10 số tự nhiên của dãy là:
$3+6+12+24+48+96+192+384+768+1536=3069$
b.
Số thứ hai: $3\times 2$
Số thứ ba: $3\times 2\times 2$
Số thứ tư: $3\times 2\times 2\times 2$
................
Số thứ 20: $3\times\underbrace{ 2\times 2\times ....\times 2}_{19}$
BT
20 tháng 4 2018
Vì dãy số nằm trong khoảng từ 1-10 nên số thứ tự của nó có giá trị bằng chính nó
Ta có: Tổng của dãy là:
(1+1)+(2+2)+(3+3)+...+(10+10) = 2(1+2+3+...+10)=2.(10.11):2=110
Đáp số: 110
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Năm số hạng đầu của dãy số: 1; 3; 5; 7; 9.
b) Công thức biểu diễn số hạng \({u_n}\) theo số hạng \({u_{n - 1}}\) là: \({u_n} = {u_{n - 1}} + 2\;\left( {n \ge 2} \right)\).
4 tháng 6 2015
Số hạng thứ m của dãy số cách đều là :
số hạng thứ m = số đầu của dãy + (m - 1). khoảng cách giữa 2 số liên tiếp.
18 tháng 9 2017
khoản cách là 3 đơn vị
khoảng cách là 3 đơn vị
khoảng cách là 4 đơn vị
ND
0
n=số hạng đầu + n-1 nhân khoảng cách