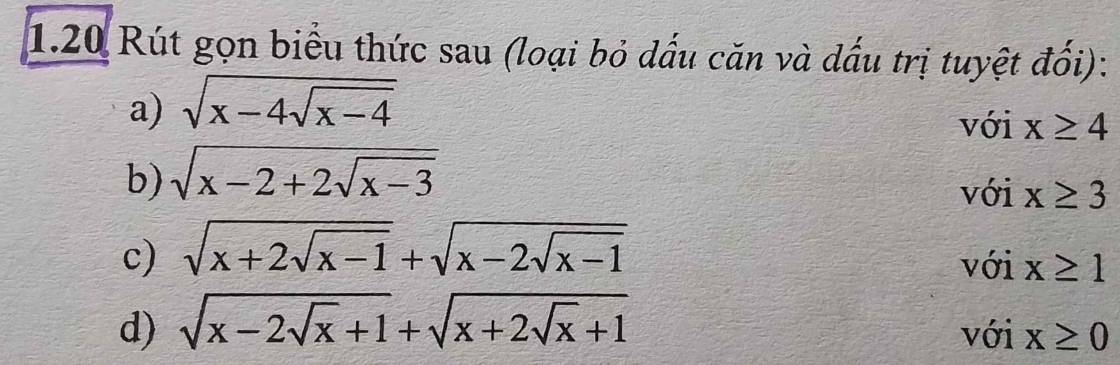 kíu tui vsssss =(((((((
kíu tui vsssss =(((((((
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


nhung phai k minh day 1 (3 điểm): Thực hiện phép tính (Tính nhanh nếu có thể)
a) 66 + 2013 + 34
b) 5 . 79 . 4 . 2 . 25
c) 5 . 23 + 711 : 79 – 12013
d) 400 : {5 [360 – (290 + 2 . 52)]}
2 (1,5 điểm): Tìm số tự nhiên x biết.
a) x +25 = 40
b) 215 – 2 (x +35) = 15
c) (2x – 3)3 = 125
3 (1,5 điểm): Cho các số sau:
24; 35; 303; 1746; 83; 2014; 1980
a) Viết tập hợp A các số chia hết cho 2 trong các số đã cho ở trên
b) Viết tập hợp B các số chia hết cho 3 trong các số đã cho ở trên
c) Tập hợp B có là tập con của tập hợp A không? Vì sao?
4 (3 điểm): Vẽ hình theo cách diễn đạt sau (chú ý: Vẽ trên cùng một hình)
a) Vẽ hai tia đối nhau Ox và Oy. Vẽ điểm A Î Ox, điểm B Î Oy,
b) Viết tên các tia trùng với tia Oy
c) Hai tia Bx và Oy có đối nhau không ? Vì sao?
d) Lấy điểm M Ï Vẽ đoạn thẳng MA, tia MO, đường thẳng MB
5 (1 điểm): Chứng minh rằng:
M = 3n+3 + 3n+1 + 2n+3 + 2n+2 ⋮6

1. The exercise which I am doing now is very interesting. Bài tập mà tôi đang làm ngay lúc này rất thú vị.
2. She is the kind of student who grasps very quickly what is taught. Cô ấy là kiểu học sinh nắm bắt rất nhanh những gì được dạy.
3. I know all the students who are standing in lines. Tôi biết tất cả các em học sinh đang đứng xếp hàng.
4. I lost the doll which I used to play with when I was a little girl. Tôi làm mất con búp bê mà tôi thường chơi khi còn là một cô bé.
5. That's the singer whose picture appeared in this morning newspaper. Đó là ca sĩ có hình ảnh xuất hiện trên tờ báo sáng nay.
6. I like the scarf which my mother bought for me on my birthday. Tôi thích chiếc khăn mà mẹ tôi đã mua cho tôi vào ngày sinh nhật của tôi.
7. I haven't finished reading all the comic books which Mai lent me last week. Tôi vẫn chưa đọc hết những cuốn truyện tranh mà Mai cho tôi mượn tuần trước.


\(\dfrac{x+1}{99}+\dfrac{x+2}{98}+\dfrac{x+3}{97}+\dfrac{x+4}{96}=-4\)
⇔\(\dfrac{x+1}{99}+1+\dfrac{x+2}{98}+1+\dfrac{x+3}{97}+\dfrac{x+4}{96}=-4+1+1+1+1\)
⇔\(\dfrac{x+1}{99}+\dfrac{99}{99}+\dfrac{x+2}{98}+\dfrac{98}{98}+\dfrac{x+3}{97}+\dfrac{97}{97}+\dfrac{x+4}{96}+\dfrac{96}{96}=-4+4\)
⇔\(\dfrac{x+100}{99}+\dfrac{x+100}{98}+\dfrac{x+100}{97}+\dfrac{x+100}{96}=0\)
⇔\(\left(x+100\right)\left(\dfrac{1}{99}+\dfrac{1}{98}+\dfrac{1}{97}+\dfrac{1}{96}\right)=0\)
⇔\(x+100=0\left(\dfrac{1}{99}+\dfrac{1}{98}+\dfrac{1}{97}+\dfrac{1}{96}\ne0\right)\)
⇔\(x=-100\)
cíu được phần 1 thôi nhé
Bổ xung ý 2
\(\dfrac{1}{x}+\dfrac{y}{3}=\dfrac{5}{6}\\ \Rightarrow\dfrac{1}{x}=\dfrac{5}{6}-\dfrac{y}{3}\\ \Rightarrow\dfrac{1}{x}=\dfrac{5-2y}{6}\\ \Rightarrow x\cdot\left(5-2y\right)=6\)
`=>x;5-2y in Ư(6)={+-1;+-3;+-2;+-6}`
mà `5-2y` là số lẻ
nên `5-2y in {+-1;+-3}`
Ta có bảng sau :
| `5-2y` | `-1` | `-3` | `1` | `3` |
| `y` | `3(T//m)` | `4(T//m)` | `2(T//m)` | `1(T//m)` |
| `x` | `-1(L)` | `-3(L)` | `1(T//m)` | `3(T//m)` |
Vậy `x;y in {(1;2);(3;1)}`

A B C H D
a)Xét \(\Delta ABC\) vuông tại A có:
\(BC^2=AC^2+AB^2\)
\(BC^2=64+36\)
\(BC^2=100\)
BC=10cm
Xét \(\Delta ABC\) có: AD là phân giác của\(\widehat{BAC}\)
=> \(\dfrac{BD}{AB}=\dfrac{DC}{AC}=\dfrac{BD+DC}{AB+AC}=\dfrac{BC}{AB+AC}=\dfrac{10}{6+8}=\dfrac{5}{7}\)
=> \(\dfrac{BD}{AB}=\dfrac{5}{7}\Leftrightarrow\dfrac{BD}{6}=\dfrac{5}{7}\Rightarrow BD=\dfrac{5}{7}.6\approx4,3\) cm
b)
Xét \(\Delta HBA\) và \(\Delta ABC\) có:
\(\widehat{B}\) chung
\(\widehat{BHA}=\widehat{BAC}\left(=90^o\right)\)
=> \(\Delta HBA\sim\)\(\Delta ABC\) (g-g)
=> \(\dfrac{AH}{AC}=\dfrac{AB}{BC}\Leftrightarrow\dfrac{AH}{8}=\dfrac{6}{10}\Rightarrow AH=\dfrac{3}{5}.8=4,8cm\)
\(\dfrac{HB}{AB}=\dfrac{AB}{BC}\Leftrightarrow\dfrac{HB}{6}=\dfrac{6}{10}\Rightarrow HB=\dfrac{3}{5}.6=3,6cm\)
c) Có : \(\dfrac{HB}{AB}=\dfrac{AB}{BC}\) ( \(\Delta HBA\sim\)\(\Delta ABC\) )
=> \(AB^2=HB.BC\)
 Ai kíu tui đy
Ai kíu tui đy





a) \(\sqrt{x-4\sqrt{x-4}}=\sqrt{\left(x-4\right)-4\sqrt{x-4}+4}=\sqrt{\left(\sqrt{x-4}-2\right)^2}=\left|\sqrt{x-4}-2\right|\)
b) \(\sqrt{x-2+2\sqrt{x-3}}=\sqrt{\left(x-3\right)+2\sqrt{x-3}+1}=\sqrt{\left(\sqrt{x-3}+1\right)^2}=\sqrt{x-3}+1\)
c) \(\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}\)
\(=\sqrt{\left(x-1\right)+2\sqrt{x-1}+1}+\sqrt{\left(x-1\right)-2\sqrt{x-1}+1}\\ =\sqrt{\left(\sqrt{x-1}+1\right)^2}+\sqrt{\left(\sqrt{x-1}-1\right)^2}\\ =\sqrt{x-1}+1+\left|\sqrt{x-1}-1\right|\)
d) \(\sqrt{x-2\sqrt{x}+1}+\sqrt{x+2\sqrt{x}+1}\)
\(=\sqrt{\left(\sqrt{x}-1\right)^2}+\sqrt{\left(\sqrt{x}+1\right)^2}\\=\left|\sqrt{x}-1\right|+\sqrt{x}+1\)
a, đk x >= 4
\(\sqrt{x-4-4\sqrt{x-4}+4}=\sqrt{\left(\sqrt{x-4}-2\right)^2}=\left|\sqrt{x-4}-2\right|=\sqrt{x-4}-2\)
b, đk x >= 3
\(\sqrt{x-3+2\sqrt{x-3}+1}=\sqrt{\left(\sqrt{x-3}+1\right)^2}=\sqrt{x-3}+1\)
c, đk x >= 1
\(\sqrt{x-1+2\sqrt{x-1}+1}+\sqrt{x-1-2\sqrt{x-1}+1}\)
\(=\sqrt{\left(\sqrt{x-1}+1\right)^2}+\sqrt{\left(\sqrt{x-1}-1\right)^2}\)
\(=\sqrt{x-1}+1+\sqrt{x-1}-1=2\sqrt{x-1}\)
d, tương tự