Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
gọi O là tâm đường tròn đường kính AB
Kẻ OE vuông góc vs CD (E thuộc CD)
suy ra E là trung điểm của CD
Mà OE là đường trung bình của hình thang ABKH (đi qua trung điểm một cạnh bên và song song vs cạnh đáy)
suy ra EH=EK mà EC=ED Suy ra đpcm
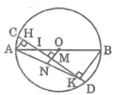
Kẻ OM ⊥ CD cắt AD tại N
Ta có: MC = MD (đường kính dây cung)
Hay MH + CH = MK + KD (1)
Ta có: OM // BK (cùng vuông góc với CD)
Hay: MN // BK
Mà: OA = OB (= R)
Suy ra: NA = NK (tính chất đường trung bình của tam giác)
Lại có: OM // AH (cùng vuông góc với CD)
Hay: MN // AH
Mà: NA = NK (chứng minh trên)
Suy ra: MH = MK (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: CH = DK
BAN TU VE HINH NHA
tu O ke OI vuong goc vs CD \(\Rightarrow CI=ID\)
de dang cm dc AH song song vs IO song song vs KB (cung vuong goc vs CD)
suy ra AHKB la hinh thang
lai co OA=OB \(\Rightarrow IH=IK\)
\(\Rightarrow IH-CI=IK-ID\Rightarrow CH=BK\)
Kẻ \(OM\perp CD\)
Vì AH // BK (cùng vuông góc HK) nên tứ giác AHKB là hình thang.
Hình thang AHKB có:
AO = OB ( bán kính )
OM // AH // BK ( cùng vuông góc HK )
=> OM là đường trung bình của hình thang.
=> MH = MK (1)
Vì OM ⊥ CD nên MC = MD (2)
Từ (1) và (2) suy ra CH = DK (đpcm)
a: Xét (O) có
ΔABC nội tiếp
AB là đường kính
Do dó: ΔABC vuông tại C
Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
Xét ΔMAB có
AC,BD là các đường cao
AC cắt BD tại H
Do đó: H là trực tâm
=>MH vuông góc vơi AB
b: Xét hình thang ABQP có
O là trung điểm của AB
ON//AP//BQ
Do đó: N là trung điểm của PQ
ΔOCD cân tại O
mà ON là đường cao
nên N là trung điểm của CD
ND+DP=NP
NC+CQ=NQ
mà ND=NC; NP=NQ
nên DP=CQ
Ta có : \(AH\perp CD\left(gt\right)\)
\(BK\perp CD\left(gt\right)\)
=> AH // BK
=> Tứ giác ABKH là hình thang có đáy AH và BK
Theo ( gt ) : OA = OB mà \(OM\perp CD\)( theo cách dựng )
=> OM // AC / BK
=> MK = MH (1)
Mặt khác : \(OM\perp CD\Rightarrow MC=MD\left(2\right)\)
Từ (1) và (2) => MH - MC = MK - MD
=> CH = DK
Vậy CH = DK
a)Tam giác BNC vuông tại N => B,N,C cùng thuộc đường tròn đường kính BC (1)
Tam giác BMC vuông tại M => B,M,C cùng thuộc đường tròn đường kính BC (2)
Từ (1) và (2) => B,N,M,C cùng thuộc đường tròn đường kính BC
b) Vì M , N thuộc đường tròn => MN là dây ( ko đi qua tâm )
=> MN < BC ( quan hệ đường kính và dây )
Kẻ OM ⊥ CD.
Vì AH // BK (cùng vuông góc HK) nên tứ giác AHKB là hình thang.
Hình thang AHKB có:
AO = OB (bán kính).
OM // AH // BK (cùng vuông góc HK)
=> OM là đường trung bình của hình thang.
=> MH = MK (1)
Vì OM ⊥ CD nên MC = MD (2)
Từ (1) và (2) suy ra CH = DK. (đpcm)
