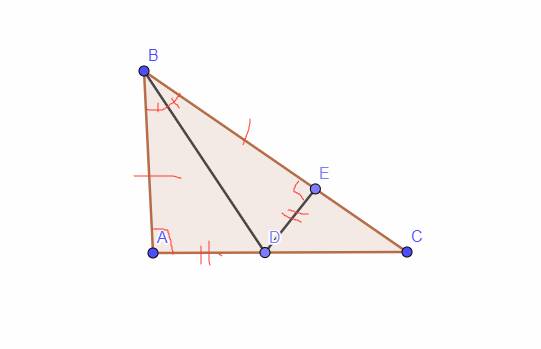
cho tam giác ABC có góc A bằng 90 độ, trên BC lấy E sao cho BA=BE.Phân giá của góc B cắt Ac tại D
a, CM: DA=DE
B, góc BED=90 độ
c, Cho BC=2AB. CM : DE là tia phân giác của góc BDC
Giups mình câu c nha!!!!!!!!!!!mình đang cần gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 12 2021
a) Xét tam giác ABD và tam giác EBD có:
+ ^ABD = ^EBD (do BD là phân giác ^B).
+ BD chung.
+ AB = BE (gt).
=> Tam giác ABD = Tam giác EBD (c - g - c).
=> DA = DE (2 cạnh tương ứng).
b) Tam giác ABD = Tam giác EBD (cmt).
=> ^BAD = ^BED (2 góc tương ứng).
Mà ^BAD = 90o (gt).
=> ^BED = 90o.
9 tháng 1 2022
a: AC=8cm
b: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
c: Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)
Do đó: ΔADK=ΔEDC
Suy ra: DK=DC
hay ΔDKC cân tại D
4 tháng 2 2023
a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔBAD=ΔBED
=>DA=DE
b: ΔBAD=ΔBED
=>góc BAD=góc BED=90 độ
=>DE vuông góc BC
c: góc EDC+góc C=90 độ
góc B+góc C=90 độ
=>góc EDC=góc ABC
15 tháng 3 2021
a) Xét ΔDAB và ΔDEB có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔDAB=ΔDEB(c-g-c)
Suy ra: DA=DE(Hai cạnh tương ứng)
6 tháng 3 2023
`a)`
Có `BD` là p/g của `hat(ABC)(GT)=>hat(B_1)=hat(B_2)`
Xét `Delta ABD` và `DElta EBD` có :
`{:(BA=BE(GT),(hat(B_1)=hat(B_2)(cmt),(BD-chung):}}`
`=>Delta ABD=Delta EBD(c.g.c)(đpcm)`
`b)`
Có `Delta ABD=Delta EBD(cmt)=>hat(A)=hat(E_1)` ( 2 góc t/ứng )
mà `hat(A)=90^0`
nên `hat(E_1)=90^0(đpcm)`
6 tháng 3 2023
`\color {blue} \text {_Namm_}`
`a,`
Xét Tam giác `ABD` và Tam giác `EBD` có:
`BA=BE (g``t)`
\(\widehat{ABD}=\widehat{EBD}\) `(` tia phân giác \(\widehat{ABE}\) `)`
`BD` chung
`=>` Tam giác `ABD =` Tam giác `EBD (c-g-c)`
`b,` Vì Tam giác `ABD =` Tam giác `EBD (a)`
`->`\(\widehat{BAD}=\widehat{BED}\) `(2` góc tương ứng `)`
Mà góc \(\widehat{A}\) vuông `(`\(\widehat{A}=90^0\) `)`
`-> `\(\widehat{BAD}=\widehat{BED}=90^0\)
`c,` Vì Tam giác `ABD =` Tam giác `EBD (a)`
`-> DE=DA (2` cạnh tương ứng `)`
Xét Tam giác `DEC:`
\(\widehat{DEC}=90^0\) `-> DC` là cạnh lớn nhất `-> DC>DE`
Mà `DE=DA -> DC>DA`
