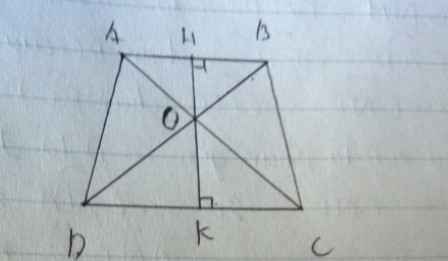
Hình thang ABCD ,AB = 2/3CD,CE = 1/3DC ,Diện tích HGF = 4cm2 .Diện tích ABCD = ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chiều cao tam giác ACD = chiều cao hình thang ABCD
Do AB = 2/3 CD nên:
Diện tích tam giác ABC = Diện tích tam giác ACD x 2/3 = 24 x 2/3 = 16 (cm2)
=> Diện tích hình thang ABCD = Diện tích tam giác ACD + Diện tích tam giác ABC
=> Diện tích hình thang ABCD = 24 + 16 = 40 (cm2)
Đ/s: 40 cm2

Bài này m dùng định lý Ta-lét đc nhưng đây là toán lớp 5 thật à"?
oa toán hình lp 5 này của bn khó quá ha, hồi mình hok lp 5 đâu có mấy kiểu này nhỉ ^^

Diện tích tam giác ADO là:
4×3=12 (cm2 )
Diện tích tam giác ABD là:
4+12=16 (cm2 )
Diện tích tam giác BCD là:
16×3=48 (cm2 )
Diện tích hình thang ABCD là:
48+16=64 (cm2 )
ĐS: 64 cm2

\(ABssCD\Rightarrow\dfrac{AB}{CD}=\dfrac{OB}{OD}=\dfrac{OA}{OC}=\dfrac{2}{3}\)
a)\(S_{AOD}=\dfrac{1}{2}OA.OD.sinAOB\)
\(S_{BOC}=\dfrac{1}{2}OB.OC.sinBOC\)
\(\Rightarrow\dfrac{S_{AOD}}{S_{BOC}}=\dfrac{OA.OD}{OB.OC}\) vì \(\widehat{AOD}=\widehat{BOC}\Rightarrow sinAOD=sinBOC\)
\(\Leftrightarrow\dfrac{S_{AOD}}{S_{BOC}}=\dfrac{2}{3}.\dfrac{3}{2}=1\)
b) vì \(ABssCD\Rightarrow\dfrac{OH}{OK}=\dfrac{2}{3}\Rightarrow\dfrac{OH}{HK}=\dfrac{2}{5}\)
\(S_{AOB}=\dfrac{1}{2}.OH.AB\\ S_{ABCD}=\dfrac{1}{2}\left(AB+CD\right).HK=\dfrac{1}{2}\left(AB+\dfrac{3}{2}AB\right).HK=\dfrac{1}{2}.\dfrac{5}{2}AB.HK\)
\(\Rightarrow\dfrac{S_{AOB}}{S_{ABCD}}=\dfrac{\dfrac{1}{2}OH.AB}{\dfrac{1}{2}HK.\dfrac{5}{2}AB}=\dfrac{2}{5}.\dfrac{1}{\dfrac{5}{2}}=\dfrac{4}{25}\)
\(\Rightarrow S_{ABCD}=\dfrac{4}{\dfrac{4}{25}}=25\)