Từ câu 03 đến câu 05.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 5 :
n Cu = a(mol) ; n Al = b(mol) ; n Mg = c(mol)
=> 64a + 27b + 24c = 11,5(1)
2Al + 6HCl $\to$ 2AlCl3 + 3H2
Mg + 2HCl $\to$ MgCl2 + H2
Theo PTHH :
n H2 = 1,5b + c = 5,6/22,4 = 0,25(2)
Bảo toàn electron :
2n SO2 = 2n Cu
2.0,1 = 2a (3)
Từ (1)(2)(3) suy ra a = 0,1 ; b = 0,1 ; c = 0,1
Vậy :
m Cu = 0,1.64 = 6,4 gam
m Al = 0,1.27 = 2,7 gam
m Mg = 0,1.24 = 2,4 gam

2.
\(d\left(I;d\right)=\dfrac{\left|1-1+2\right|}{\sqrt{1^2+1^2}}=\sqrt{2}\)
Gọi H là trung điểm AB \(\Rightarrow IH\perp AB\)
\(\Rightarrow IH=d\left(I;d\right)\)
Áp dụng định lý Pitago:
\(IA^2=IH^2+AH^2\Leftrightarrow R^2=IH^2+\left(\dfrac{AB}{2}\right)^2\)
\(\Rightarrow R^2=3\)
Phương trình (C):
\(\left(x-1\right)^2+\left(y+1\right)^2=3\)
3.
Đường tròn (C) tâm \(I\left(1;1\right)\) bán kính \(R=4\)
Gọi H là trung điểm MN \(\Rightarrow IH\perp MN\)
\(S_{IMN}=\dfrac{1}{2}IN.IM.sin\widehat{MIN}=\dfrac{1}{2}R^2.sin\widehat{MIN}\)
\(\Rightarrow S_{max}\) khi \(sin\widehat{MIN}\) đạt max
Ta có: \(\overrightarrow{IA}=\left(1;-1\right)\Rightarrow IA=\sqrt{2}\)
\(\Rightarrow MN\ge2\sqrt{R^2-IA^2}=2\sqrt{14}\)
\(\Rightarrow cos\widehat{MIN}=\dfrac{IM^2+IN^2-MN^2}{2IM.IN}=\dfrac{2R^2-MN^2}{2R^2}\le\dfrac{2.4^2-4.14}{2.4^2}=-\dfrac{3}{4}< 0\)
\(\Rightarrow180^0\le\widehat{MIN}< 90^0\)
\(\Rightarrow sin\widehat{MIN}\) nghịch biến \(\Rightarrow sin\widehat{MIN}\) đạt GTLN khi \(\widehat{MIN}\) đạt GTNN
\(\Rightarrow\widehat{MIH}=\dfrac{1}{2}\widehat{MIN}\) đạt GTNN
Do \(180^0\le\widehat{MIN}< 90^0\Rightarrow90^0\le\widehat{MIH}< 45^0\)
\(\Rightarrow sin\widehat{MIH}\) đồng biến \(\Rightarrow\widehat{MIH}\) đạt GTNN khi \(sin\widehat{MIH}\) đạt GTNN
\(sin\widehat{MIH}=\dfrac{MH}{IM}=\dfrac{MN}{2R}\ge\dfrac{\sqrt{14}}{4}\)
Dấu "=" xảy ra khi và chỉ khi H trùng A
\(\Rightarrow d\perp IA\Rightarrow d\) nhận (1;-1) là 1 vtpt
Phương trình d:
\(1\left(x-2\right)-1\left(y-0\right)=0\Leftrightarrow x-y-2=0\)

1.
Phương trình có 2 nghiệm khi:
\(\left\{{}\begin{matrix}m\ne0\\\Delta'\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\\left(m-2\right)^2-m\left(m-3\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\-m+4\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\m\le4\end{matrix}\right.\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-2\right)}{m}\\x_1x_2=\dfrac{m-3}{m}\end{matrix}\right.\)
\(x_1+x_2+x_1x_2\ge2\)
\(\Leftrightarrow\dfrac{2\left(m-2\right)}{m}+\dfrac{m-3}{m}-2\ge0\)
\(\Leftrightarrow\dfrac{m-7}{m}\ge0\)
\(\Rightarrow\left[{}\begin{matrix}m\ge7\\m< 0\end{matrix}\right.\)
\(\Rightarrow m< 0\)
2.
\(T=\dfrac{\left(sinx+cosx\right)\left(sin^2x+cos^2x-sinx.cosx\right)}{sinx+cosx}+sinx.cosx\)
\(=1-sinx.cosx+sinx.cosx=1\)
3.
\(\dfrac{sinx}{cosx}+\dfrac{cosx}{sinx}=3\Leftrightarrow\dfrac{sin^2x+cos^2x}{sinx.cosx}=3\)
\(\Leftrightarrow\dfrac{1}{sinx.cosx}=3\Leftrightarrow sinx.cosx=\dfrac{1}{3}\Leftrightarrow2sinx.cosx=\dfrac{2}{3}\)
\(\Leftrightarrow sin2x=\dfrac{2}{3}\)
\(0< x< \dfrac{\pi}{4}\Rightarrow0< 2x< \dfrac{\pi}{2}\Rightarrow cos2x>0\)
\(\Rightarrow cos2x=\sqrt{1-sin^22x}=\dfrac{\sqrt{5}}{3}\)

1.
Với \(m=2\Rightarrow\) pt có nghiệm \(x=-2\) (thỏa mãn)
Với \(m\ne2\) pt đã cho có nghiệm khi:
\(\Delta'=\left(2m-3\right)^2-\left(m-2\right)\left(5m-6\right)\ge0\)
\(\Leftrightarrow-m^2+4m-3\ge0\Rightarrow1\le m\le3\)
Vậy \(1\le m\le3\)
b.
Để pt có 2 nghiệm pb \(\Leftrightarrow\left\{{}\begin{matrix}1< m< 3\\m\ne2\end{matrix}\right.\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-4m+6}{m-2}\\x_1x_2=\dfrac{5m-6}{m-2}\end{matrix}\right.\)
\(x_1+x_2+x_1x_2>2013\)
\(\Leftrightarrow\dfrac{-4m+6}{m-2}+\dfrac{5m-6}{m-2}>2013\)
\(\Leftrightarrow\dfrac{m}{m-2}>2013\)
\(\Leftrightarrow\dfrac{-2012m+4026}{m-2}>0\)
\(\Leftrightarrow2< m< \dfrac{2013}{1006}\)
2.
\(\overrightarrow{AB}=\left(7;7\right)=7\left(1;1\right)\)
Gọi M là trung điểm AB \(\Rightarrow M\left(\dfrac{3}{2};\dfrac{1}{2}\right)\)
Phương trình trung trực của AB có dạng:
\(1\left(x-\dfrac{3}{2}\right)+1\left(y-\dfrac{1}{2}\right)=0\Leftrightarrow x+y-2=0\)
I là tâm đường tròn \(\Rightarrow\) I thuộc trung trực của AB
\(\Rightarrow\) Tọa độ của I là nghiệm: \(\left\{{}\begin{matrix}x+y-2=0\\-x+y-2=0\end{matrix}\right.\) \(\Rightarrow I\left(0;2\right)\)
\(\Rightarrow\overrightarrow{IA}=\left(-2;-5\right)\Rightarrow R^2=IA^2=29\)
Phương trình đường tròn:
\(x^2+\left(y-2\right)^2=29\)

1.
\(\dfrac{3\pi}{2}< a< 2\pi\Rightarrow\left\{{}\begin{matrix}sina< 0\\cosa>0\end{matrix}\right.\)
\(1+tan^2a=\dfrac{1}{cos^2a}\Rightarrow cosa=\sqrt{\dfrac{1}{1+tan^2a}}=\dfrac{\sqrt{26}}{26}\)
\(sina=-\sqrt{1-cos^2a}=-\dfrac{5\sqrt{26}}{26}\)
\(sin\left(a-\dfrac{2\pi}{3}\right)=sina.cos\left(\dfrac{2\pi}{3}\right)-cosa.sin\left(\dfrac{2\pi}{3}\right)=\dfrac{-\sqrt{78}-5\sqrt{26}}{52}\)
2.
Đường tròn tiếp xúc trục Ox \(\Rightarrow R=d\left(I;Ox\right)=\left|y_I\right|=2\)
Phương trình: \(\left(x+3\right)^2+\left(y-2\right)^2=4\)
3.
\(\overrightarrow{AB}=\left(1;1\right)\)
CH vuông góc AB nên nhận (1;1) là 1 vtpt
Phương trình CH:
\(1\left(x+1\right)+1\left(y-4\right)=0\Leftrightarrow x+y-3=0\)
N là trung điểm BC \(\Rightarrow N\left(1;2\right)\Rightarrow\overrightarrow{AN}=\left(-1;3\right)\)
\(\Rightarrow\) Đường thẳng AN nhận (3;1) là 1 vtpt
Phương trình AN:
\(3\left(x-2\right)+1\left(y+1\right)=0\Leftrightarrow3x+y-5=0\)

1/
\(4FeS_2 + 11O_2 \xrightarrow{t^o} 2Fe_2O_3 + 8SO_2\\ SO_2 + 2H_2S \to 3S + 2H_2O\\ S + H_2 \xrightarrow{t^o,xt} H_2S\\ H_2S + 4Br_2 + 4H_2O \to 8HBr + H_2SO_4\\ H_2SO_4 + NaCl \xrightarrow{t^o} NaHSO_4 + HCl\\ MnO_2 + 4HCl \to MnCl_2 + Cl_2 + 2H_2O\\ 2Na +C l_2 \xrightarrow{t^o} 2NaCl\\ NaCl + AgNO_3 \to AgCl + NaNO_3\)
2/
\(S + H_2 \xrightarrow{t^o} H_2S\\ H_2S + \dfrac{3}{2}O_2 \xrightarrow{t^o} SO_2 + H_2O\\ 2SO_2 +O_2 \xrightarrow{t^o,xt} 2SO_3\\ SO_3 + H_2O \to H_2SO_4\\ CuO + H_2SO_4 \to CuSO_4 + H_2O\\ CuSO_4 + BaCl_2 \to BaSO_4 + CuCl)2\)
1)
4FeS2 + 11O2 -to-> 2Fe2O3 + 8SO2
SO2 + 2H2S -to-> 3S + 2H2O
S + H2 -to-> H2S
H2S + 4Br2 + 4H2O => H2SO4 + 8HBr
BaCl2 + H2SO4 => BaSO4 + 2HCl
2HCl-dp-> H2 + Cl2
Na + 1/2Cl2 -to-> NaCl
NaCl + AgNO3 => AgCl + NaNO3
2)
H2 + S -to-> H2S
2H2S + 3O2 -to-> 2SO2 + 2H2O
SO2 + 1/2O2 -to,V2O5-> SO3
SO3 + H2O => H2SO4
H2SO4 + CuO => CuSO4 + H2O
CuSO4 + BaCl2 => BaSO4 + CuCl2

tham khảo
a,Đường, muối và muối nở là những chất tinh khiết là hợp chất. Chất tinh khiết là tinh thể gồm: Muối, kim cương, tinh thể protein, tinh thể đồng sunfat. Hỗn hợp đồng nhất có thể được coi là ví dụ của các chất tinh khiết như: dầu thực vật, mật ong và không khí.
b,Hỗn hợp mayonnaise là một dạng khác, không phải huyền phù mà là nhũ tương.
Nước đường là hỗn hợp gồm nước và đường.
- Không khí là hỗn hợp gồm các khí O2; N2 và lượng nhỏ các khí khác.
SÀ CÂN TRỘN MA TUÝ







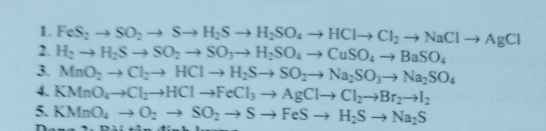
3.
\(\pi< a< \dfrac{3\pi}{2}\Rightarrow cosa< 0\)
\(\Rightarrow cosa=-\sqrt{1-sin^2a}=-\dfrac{4}{5}\)
b.
\(\dfrac{2+2cos2a-sin2a}{sin2a-sin^2a}=\dfrac{2+2\left(2cos^2a-1\right)-2sina.cosa}{2sina.cosa-sin^2a}\)
\(=\dfrac{4cos^2a-2sina.cosa}{sina\left(2cosa-sina\right)}=\dfrac{2cosa\left(2cosa-sina\right)}{sina\left(2cosa-sina\right)}=\dfrac{2cosa}{sina}=2cota\)
4.
\(\overrightarrow{BA}=\left(2;3\right)\Rightarrow\) đường thẳng d nhận (3;-2) là 1 vtpt
Phương trình d:
\(3\left(x-4\right)-2\left(y+1\right)=0\Leftrightarrow3x-2y-14=0\)
5.
Đường thẳng BC vuông góc đường cao kẻ từ A nên nhận (1;-1) là 1 vtpt
Phương trình BC:
\(1\left(x+1\right)-1\left(y-2\right)=0\Leftrightarrow x-y+3=0\)
C là giao điểm BC và trung tuyến kẻ từ C nên là nghiệm:
\(\left\{{}\begin{matrix}x-y+3=0\\2x-y+1=0\end{matrix}\right.\) \(\Rightarrow C\left(2;5\right)\)
Do M là trung điểm BC
\(\Rightarrow\left\{{}\begin{matrix}x_B=2x_M-x_C=-4\\y_B=2y_M-y_C=-1\end{matrix}\right.\) \(\Rightarrow B\left(-4;-1\right)\)
Do A thuộc đường cao kẻ từ A nên tọa độ có dạng: \(A\left(a;4-a\right)\)
Gọi N là trung điểm AB \(\Rightarrow N\left(\dfrac{a-4}{2};\dfrac{3-a}{2}\right)\)
N thuộc trung tuyến kẻ từ C nên tọa độ thỏa mãn:
\(2\left(\dfrac{a-4}{2}\right)-\left(\dfrac{3-a}{2}\right)+1=0\Rightarrow a=3\) \(\Rightarrow A\left(3;1\right)\)