Tìm min A = x2 + 2x + 5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NP
1
27 tháng 6 2021
Không có max
`a)sqrt{x^2-2x+5}`
`=sqrt{x^2-2x+1+4}`
`=sqrt{(x-1)^2+4}`
Vì `(x-1)^2>=0`
`=>(x-1)^2+4>=4`
`=>sqrt{(x-1)^2+4}>=sqrt4=2`
Dấu "=" xảy ra khi `x=1.`
`b)2+sqrt{x^2-4x+5}`
`=2+sqrt{x^2-4x+4+1}`
`=2+sqrt{(x-2)^2+1}`
Vì `(x-2)^2>=0`
`=>(x-2)^2+1>=1`
`=>sqrt{(x-2)^2+1}>=1`
`=>sqrt{(x-2)^2+1}+2>=3`
Dấu "=" xảy ra khi `x=2`
TN
22 tháng 7 2023
A=(\(x^4\)-2\(x^2\)+1)+(\(x^2\)+2x+1)+5
A=\((x^2-1)^2+(x+1 )^2+5\)\(\ge\)\(5\)
Dấu bằng xảy ra\(\Leftrightarrow\)\(\begin{cases} x^2-1=0\\ x+1=0 \end{cases} \)
\(\Leftrightarrow\)\(x=-1\)
Vậy Amin=5 \(\Leftrightarrow\)x=-1
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1 2021
\(A=\dfrac{51x^2+136x+102}{17\left(x^2-2x+1\right)}=\dfrac{2\left(x^2-2x+1\right)+49x^2+140x+100}{17\left(x^2-2x+1\right)}\)
\(A=\dfrac{2}{17}+\dfrac{\left(7x+10\right)^2}{17\left(x-1\right)^2}\ge\dfrac{2}{17}\)
\(A_{min}=\dfrac{2}{17}\) khi \(x=-\dfrac{10}{7}\)
NT
1
7 tháng 10 2023
`#3107.101107`
a)
`x^2 + 6x + 10`
`= (x^2 + 2*x*3 + 3^2) + 1`
`= (x + 3)^2 + 1`
Vì `(x + 3)^2 \ge 0` `AA` `x`
`=> (x + 3)^2 + 1 \ge 1` `AA` `x`
Vậy, GTNN của bt là 1 khi `(x + 3)^2 = 0`
`<=> x + 3 = 0`
`<=> x = -3`
b)
`4x^2 - 4x + 5`
`= [(2x)^2 - 2*2x*1 + 1^2] + 4`
`= (2x - 1)^2 + 4`
Vì `(2x - 1)^2 \ge 0` `AA` `x`
`=> (2x - 1)^2 + 4 \ge 4` `AA` `x`
Vậy, GTNN của bt là `4` khi `(2x - 1)^2 = 0`
`<=> 2x - 1 = 0`
`<=> 2x = 1`
`<=> x = 1/2`
c)
`x^2 - 3x + 1`
`= (x^2 - 2*x*3/2 + 9/4) - 5/4`
`= (x - 3/2)^2 - 5/4`
Vì `(x - 3/2)^2 \ge 0` `AA` `x`
`=> (x - 3/2)^2 - 5/4 \ge -5/4` `AA` `x`
Vậy, GTNN của bt là `-5/4` khi `(x - 3/2)^2 = 0`
`<=> x - 3/2 = 0`
`<=> x = 3/2`
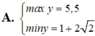
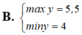
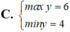
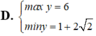
x2+2x+5= x2+2x+1+1
=(x+1)2+4
vì ( x+1)2 >=0 ( với mọi x)
nên (x+1)2+4>= 4 với mọi x
dấu bằng xảy ra khi và chỉ khi
x+1=0
=. x=-1
min A=4