CHO (a,b)=1 .Chứng minh :
a) (a,a-b)=1
b)(ab,a+b) =1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) Chú ý m > 2 thì m > 0.
b) Chú ý a < 0 và b < 0 thì ab > 0. Khi đó a > b, nhân hai vế với 1 ab > 0 ta thu được 1 b > 1 a . Tương tự a > 0, b > 0, a > b ta được 1 a < 1 b .

a) Biến đổi vế trái:
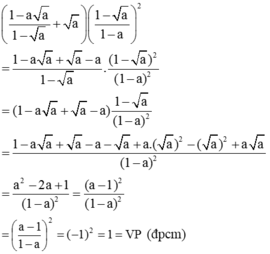
b) Biến đổi vế trái:
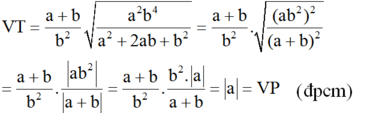
( v ì a + b > 0 n ê n | a + b | = a + b ; b 2 > 0 )

a: \(A=\left(\dfrac{1}{99}+1\right)+\left(\dfrac{2}{98}+1\right)+...+\left(\dfrac{98}{2}+1\right)+1\)
\(=\dfrac{100}{99}+\dfrac{100}{98}+...+\dfrac{100}{2}+\dfrac{100}{100}\)
\(=100\cdot\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{100}\right)\)=100B
=>B/A=1/100
b: \(A=\left(\dfrac{1}{49}+1\right)+\left(\dfrac{2}{48}+1\right)+\left(\dfrac{3}{47}+1\right)+...+\left(\dfrac{48}{2}+1\right)+\left(1\right)\)
\(=\dfrac{50}{49}+\dfrac{50}{48}+....+\dfrac{50}{2}+\dfrac{50}{50}\)
\(=50\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{50}\right)\)
\(B=\dfrac{2}{2}+\dfrac{2}{3}+\dfrac{2}{4}+...+\dfrac{2}{49}+\dfrac{2}{50}\)
\(=2\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{49}+\dfrac{1}{50}\right)\)
=>A/B=25

\(\dfrac{9}{4}=ab+a+b+1\le\dfrac{1}{4}\left(a+b\right)^2+a+b+1\)
\(\Leftrightarrow\left(a+b\right)^2+4\left(a+b\right)-5\ge0\)
\(\Leftrightarrow\left(a+b-1\right)\left(a+b+5\right)\ge0\)
\(\Leftrightarrow a+b-1\ge0\) (do \(a+b+5>0\))
\(\Rightarrow a+b\ge1\)
b.
\(a^2+b^2\ge\dfrac{1}{2}\left(a+b\right)^2\ge\dfrac{1}{2}.1^2=\dfrac{1}{2}\) (đpcm)