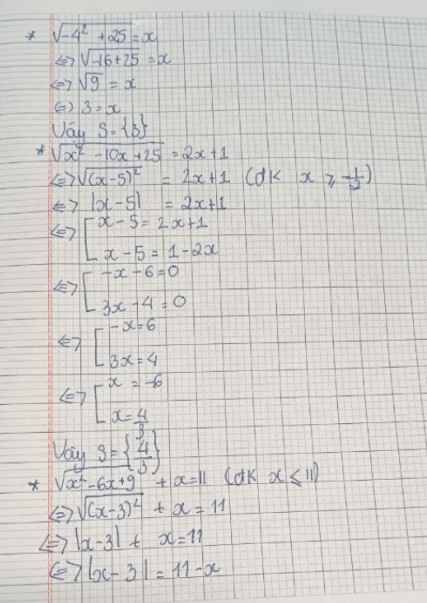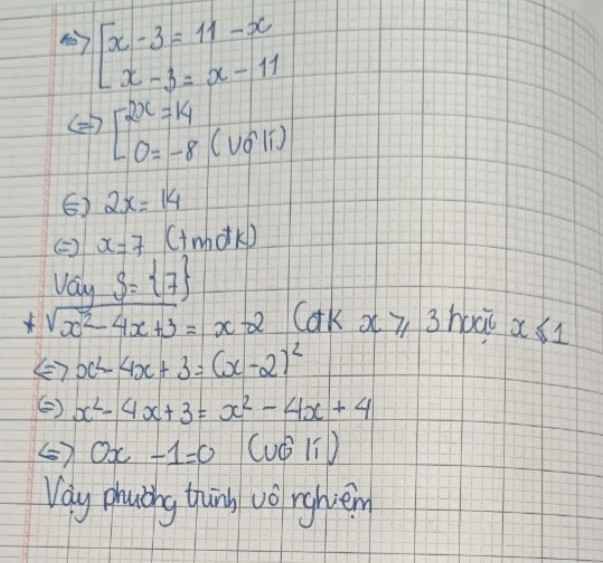4(x4+4x+2)=11\(\sqrt{x^4+4}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 9 2023
c) \(\sqrt[]{8+\sqrt[]{x}}+\sqrt{5-\sqrt[]{x}}=5\)
\(\Leftrightarrow\left(\sqrt[]{8+\sqrt[]{x}}+\sqrt{5-\sqrt[]{x}}\right)^2=25\left(1\right)\left(đkxđ:0\le x\le25\right)\)
Áp dụng Bất đẳng thức Bunhiacopxki cho 2 cặp số dương \(\left(1;\sqrt[]{8+\sqrt[]{x}}\right);\left(1;\sqrt{5-\sqrt[]{x}}\right)\)
\(\left(1.\sqrt[]{8+\sqrt[]{x}}+1.\sqrt{5-\sqrt[]{x}}\right)^2\le\left(1^2+1^2\right)\left(8+\sqrt[]{x}+5-\sqrt[]{x}\right)=26\)
\(\left(1\right)\Leftrightarrow26=25\left(vô.lý\right)\)
Vậy phương trình đã cho vô nghiệm
b) \(\sqrt[]{1+4x}+2\sqrt[]{2-x}+2\sqrt[]{\left(1+4x\right)\left(2-x\right)}=3\) \(\left(đkxđ:-\dfrac{1}{4}\le x\le2\right)\)
\(\)\(\Leftrightarrow\sqrt[]{1+4x}+2\sqrt[]{2-x}=3-2\sqrt[]{\left(1+4x\right)\left(2-x\right)}\)
\(\Leftrightarrow\left(\sqrt[]{1+4x}+2\sqrt[]{2-x}\right)^2=\left[3-2\sqrt[]{\left(1+4x\right)\left(2-x\right)}\right]^2\left(1\right)\)
Áp dụng Bất đẳng thức Bunhiacopxki :
\(\left(1.\sqrt[]{1+4x}+2\sqrt[]{2-x}\right)^2\le\left(1^2+2^2\right)\left(1+4x+2-x\right)=5\left(3x+3\right)\)
Áp dụng Bất đẳng thức Cauchy :
\(2\sqrt[]{\left(1+4x\right)\left(2-x\right)}\le1+4x+2-x=3x+3\)
Dấu "=" xảy ra khi và chỉ khi
\(1+4x=2-x\)
\(\Leftrightarrow x=\dfrac{1}{5}\left(thỏa.đk\right)\)
\(pt\left(1\right)\Leftrightarrow5\left(4x+3\right)=4x+3\)
\(\Leftrightarrow4\left(4x+3\right)=0\)
\(\Leftrightarrow x=-\dfrac{3}{4}\left(k.thỏa.x=\dfrac{1}{5}.vô.lý\right)\)
Vậy phương trình đã cho vô nghiệm
Y
28 tháng 6 2023
\(a,P=\left(\dfrac{\sqrt{x}+2}{\sqrt{x}-2}-\dfrac{\sqrt{x}-2}{\sqrt{x}+2}-\dfrac{4x}{4-x}\right):\dfrac{x+5\sqrt{x}+6}{x-4}\left(dk:x\ge0,x\ne4\right)\)
\(=\left(\dfrac{\sqrt{x}+2}{\sqrt{x}-2}-\dfrac{\sqrt{x}-2}{\sqrt{x}+2}+\dfrac{4x}{x-4}\right).\dfrac{x-4}{x+2\sqrt{x}+3\sqrt{x}+6}\)
\(=\dfrac{\left(\sqrt{x}+2\right)^2-\left(\sqrt{x}-2\right)^2+4x}{x-4}.\dfrac{x-4}{\sqrt{x}\left(\sqrt{x}+2\right)+3\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x+4\sqrt{x}+4-x+4\sqrt{x}-4+4x}{\left(\sqrt{x}+3\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{4x+8\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{4\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{4\sqrt{x}}{\sqrt{x}+3}\)
\(b,x=\sqrt{9+4\sqrt{5}}-\sqrt{9-4\sqrt{4}}\\ =\sqrt{\left(\sqrt{5}+2\right)^2}-\sqrt{\left(\sqrt{5}-2\right)^2}\\ =\left|\sqrt{5}+2\right|-\left|\sqrt{5}-2\right|\\ =\sqrt{5}+2-\sqrt{5}+2\\ =4\)
Khi \(x=4\Rightarrow P=\dfrac{4\sqrt{4}}{\sqrt{4}+3}=\dfrac{4.2}{2+3}=\dfrac{8}{5}\)
\(c,P=2\Leftrightarrow\dfrac{4\sqrt{x}}{\sqrt{x}+3}=2\Leftrightarrow\dfrac{4\sqrt{x}-2\left(\sqrt{x}+3\right)}{\sqrt{x}+3}=0\Leftrightarrow2\sqrt{x}-6=0\Leftrightarrow\sqrt{x}=3\Leftrightarrow x=9\)
Y
2 tháng 7 2023
Câu b bạn có bị lỗi dấu căn không mà sao nó kéo dài cả 2 vế pt vậy :v
\(a,\sqrt{x^2-6x+9}+x=11\\ \Leftrightarrow\sqrt{\left(x-3\right)^2}=11-x\)
\(\Leftrightarrow\left|x-3\right|=11-x\\ TH_1:x\ge3\\ x-3=11-x\\ \Leftrightarrow2x=14\\ \Leftrightarrow x=7\left(tm\right)\)
\(TH_2:x< 3\\ -x+3=11-x\\ \Leftrightarrow-x+x=11-3\\ \Leftrightarrow0=8\left(VL\right)\)
Vậy \(S=\left\{7\right\}\)
\(c,\sqrt{16\left(x+1\right)}-\sqrt{9\left(x+1\right)}=4\) \(\left(dk:x\ge-1\right)\)
\(\Leftrightarrow\sqrt{4^2}.\sqrt{\left(x+1\right)}-\sqrt{3^2}.\sqrt{\left(x+1\right)}=4\left(1\right)\)
Đặt \(a=\sqrt{x+1}\left(a\ge0\right)\)
Pt trở thành : \(4a-3a=4\Leftrightarrow a=4\left(tmdk\right)\)
\(\Rightarrow\sqrt{x+1}=4\\ \Rightarrow\left(\sqrt{x+1}\right)^2=16\\ \Rightarrow\left|x+1\right|=16\)
\(TH_1:x\ge-1\\ x+1=16\Leftrightarrow x=15\left(tm\right)\\ TH_2:x< -1\\ -x-1=16\Leftrightarrow x=-17\left(tm\right)\)
Nhưng loại TH2 vì dk ban đầu là \(x\ge-1\)
Vậy \(S=\left\{15\right\}\)
\(d,\sqrt{9x+9}+\sqrt{4x+4}=\sqrt{x+1}\left(dk:x\ge-1\right)\\ \Leftrightarrow\sqrt{9}.\sqrt{x+1}+\sqrt{4}.\sqrt{x+1}-\sqrt{x+1}=0\)
Đặt \(\sqrt{x+1}=a\left(a\ge0\right)\)
Tới đây bạn làm tương tự câu c nha.
17 tháng 6 2021
a) ĐKXĐ : \(x\ge-3\)\(pt\Leftrightarrow x^2-2x+1=x+3-4\sqrt{x+3}+4\Leftrightarrow\left(x-1\right)^2=\left(\sqrt{x+3}-2\right)^2\Leftrightarrow x-1=\sqrt{x+3}-2\Leftrightarrow x+1=\sqrt{x+3}\Leftrightarrow\left(x+1\right)^2=x+3\left(x\ge-1\right)\Leftrightarrow x^2+2x+1=x+3\Leftrightarrow x^2+x-2=0\Leftrightarrow\left[{}\begin{matrix}x=1\left(tmdk\right)\\x=-2\left(kotm\right)\end{matrix}\right.\)
D
21 tháng 6 2019
a) ĐK:\(x\ge\frac{1}{2}\)
Với \(x\ge\frac{1}{2}\) thì \(\left\{{}\begin{matrix}\sqrt{4x-1}\ge1\\\sqrt{4x^2-1}\ge0\end{matrix}\right.\Rightarrow VT\ge1=VP\)
=> PT có nghiệm khi và chỉ khi \(x=\frac{1}{2}\)
b) ĐK: \(-3\le x\le\frac{3}{2}\)
\(x+4\sqrt{x+3}+2\sqrt{3-2x}=11\\ \left[\left(x+3\right)-4\sqrt{x+3}+4\right]+\left[\left(3-2x\right)-2\sqrt{3-2x}+1\right]=0\\ \left(\sqrt{x+3}-2\right)^2+\left(\sqrt{3-2x}-1\right)^2=0\)
Lập luận =>\(\left\{{}\begin{matrix}\sqrt{x+3}=2\\\sqrt{3-2x}=1\end{matrix}\right.\Leftrightarrow x=1}\)
CS
1
8 tháng 10 2016
\(4\left(x^2+4x+2\right)=11\sqrt{x^4+4}\)
\(\Leftrightarrow4\left(x^2+4x+2\right)=11\sqrt{\left(x^2-x+2\right)\left(x^2+x+2\right)}\)
\(\Leftrightarrow2\left(x^2-x+2\right)+2\left(x^2+x+2\right)+16x=11\sqrt{\left(x^2-x+2\right)\left(x^2+x+2\right)}\)
Nhận thấy x = 0 không là nghiệm của pt trên, ta chia cả hai vế của pt cho x được
\(2\left(x+\frac{2}{x}-1\right)+2\left(x+\frac{2}{x}+1\right)+16=11\sqrt{\left(x+\frac{2}{x}-1\right)\left(x+\frac{2}{x}+1\right)}\)
Đặt \(a=\sqrt{x+\frac{2}{x}-1}\) , \(b=\sqrt{x+\frac{2}{x}+1}\) thì
\(\hept{\begin{cases}2a^2+2b^2+16=11ab\\b^2-a^2=2\end{cases}}\)
Bạn giải hệ trên để tìm a,b rồi suy ra x nhé :)
P
21 tháng 12 2023
Bài 3:
a) \(\sqrt{3x-2}=4\)
⇔\(\sqrt{3x-2}=\sqrt{4^2}\)
⇔\(3x-2=4^2=16\)
\(3x=16+2=18\)
\(x=18:3=6\)
Vậy \(x=6\)
b)\(\sqrt{4x^2+4x+1}-11=5\)
⇔\(\sqrt{\left(2x\right)^2+2\left(2x\right)\cdot1+1^2}-11=5\)
⇔\(\sqrt{\left(2x+1\right)^2}-11=5\)
TH1:
⇔\(\left(2x+1\right)-11=5\)
\(2x+1=5+11=16\)
\(2x=16-1=15\)
\(x=15:2=7,5\)
TH2:
⇔\(\left(2x+1\right)-11=-5\)
\(2x-1=-5+11=6\)
\(2x=6+1=7\)
\(x=7:2=3,5\)
Vậy \(x=\left\{7,5;3,5\right\}\)
(Câu này mình không chắc chắn lắm)
(Học sinh lớp 6 đang làm bài này)
21 tháng 12 2023
Bài 4:
a: \(C=\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right)\left(\dfrac{\sqrt{x}}{\sqrt{x}+1}+\dfrac{\sqrt{x}}{\sqrt{x}-1}\right)\)
\(=\dfrac{x-1}{\sqrt{x}}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)+\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-\sqrt{x}+x+\sqrt{x}}{\sqrt{x}}=\dfrac{2x}{\sqrt{x}}=2\sqrt{x}\)
b: C-6<0
=>C<6
=>\(2\sqrt{x}< 6\)
=>\(\sqrt{x}< 3\)
=>0<=x<9
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}0< x< 9\\x\ne1\end{matrix}\right.\)