giải phương trình: 4x2 + \(\sqrt{2x+1}\) + 6 = 12x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 9 2018
a) Phương trình 4 x 2 + 2 x − 5 = 0
Có a = 4; b = 2; c = -5, a.c < 0
⇒ Phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-et ta có: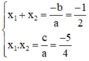 
b) Phương trình . 9 x 2 − 12 x + 4 = 0
Có a = 9; b' = -6; c = 4 ⇒ Δ 2 = ( - 6 ) 2 - 4 . 9 = 0
⇒ Phương trình có nghiệm kép x 1 = x 2 .
Theo hệ thức Vi-et ta có: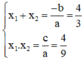 
c) Phương trình 5 x 2 + x + 2 = 0
Có a = 5; b = 1; c = 2 ⇒ Δ = 1 2 − 4.2.5 = − 39 < 0
⇒ Phương trình vô nghiệm.
d) Phương trình 159 x 2 − 2 x − 1 = 0
Có a = 159; b = -2; c = -1; a.c < 0
⇒ Phương trình có hai nghiệm phân biệt x 1 ; x 2 .
Theo hệ thức Vi-et ta có: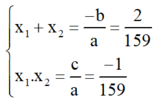 
LP
2
5 tháng 3 2022
1.\(\left(x+2\right)\left(2x-3\right)=x^2-4\)
\(\Leftrightarrow\left(x+2\right)\left(2x-3\right)-\left(x+2\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(2x-3-x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\)
2.\(x^2+3x+2=0\)
\(\Leftrightarrow x^2+x+2x+2=0\)
\(\Leftrightarrow x\left(x+1\right)+2\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-2\end{matrix}\right.\)
3.\(2x^2+5x+3=0\)
\(\Leftrightarrow2x^2+2x+3x+3=0\)
\(\Leftrightarrow2x\left(x+1\right)+3\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(2x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{3}{2}\end{matrix}\right.\)
4.\(x^3+x^2-12x=0\)
\(\Leftrightarrow x\left(x^2+x-12\right)=0\)
\(\Leftrightarrow x\left(x+4\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-4\\x=3\end{matrix}\right.\)
5 tháng 3 2022
a: \(\Leftrightarrow\left(x+2\right)\left(2x-3\right)-\left(x+2\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(2x-3-x+2\right)=0\)
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
b: =>(x+1)(x+2)=0
=>x=-1 hoặc x=-2
c: =>(2x+3)(x+1)=0
=>x=-1 hoặc x=-3/2
d: =>x(x+4)(x-3)=0
hay \(x\in\left\{0;-4;3\right\}\)
MP
1
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 1 2021
ĐKXĐ: ...
\(VT\le\sqrt{2\left(2x-3+5-2x\right)}=2\)
\(VP=3\left(x-2\right)^2+2\ge2\)
Dấu "=" xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}2x-3=5-2x\\x-2=0\end{matrix}\right.\) \(\Leftrightarrow x=2\)
25 tháng 11 2023
2: ĐKXĐ: x>=0
\(\sqrt{3x}-2\sqrt{12x}+\dfrac{1}{3}\cdot\sqrt{27x}=-4\)
=>\(\sqrt{3x}-2\cdot2\sqrt{3x}+\dfrac{1}{3}\cdot3\sqrt{3x}=-4\)
=>\(\sqrt{3x}-4\sqrt{3x}+\sqrt{3x}=-4\)
=>\(-2\sqrt{3x}=-4\)
=>\(\sqrt{3x}=2\)
=>3x=4
=>\(x=\dfrac{4}{3}\left(nhận\right)\)
3:
ĐKXĐ: x>=0
\(3\sqrt{2x}+5\sqrt{8x}-20-\sqrt{18}=0\)
=>\(3\sqrt{2x}+5\cdot2\sqrt{2x}-20-3\sqrt{2}=0\)
=>\(13\sqrt{2x}=20+3\sqrt{2}\)
=>\(\sqrt{2x}=\dfrac{20+3\sqrt{2}}{13}\)
=>\(2x=\dfrac{418+120\sqrt{2}}{169}\)
=>\(x=\dfrac{209+60\sqrt{2}}{169}\left(nhận\right)\)
4: ĐKXĐ: x>=-1
\(\sqrt{16x+16}-\sqrt{9x+9}=1\)
=>\(4\sqrt{x+1}-3\sqrt{x+1}=1\)
=>\(\sqrt{x+1}=1\)
=>x+1=1
=>x=0(nhận)
5: ĐKXĐ: x<=1/3
\(\sqrt{4\left(1-3x\right)}+\sqrt{9\left(1-3x\right)}=10\)
=>\(2\sqrt{1-3x}+3\sqrt{1-3x}=10\)
=>\(5\sqrt{1-3x}=10\)
=>\(\sqrt{1-3x}=2\)
=>1-3x=4
=>3x=1-4=-3
=>x=-3/3=-1(nhận)
6: ĐKXĐ: x>=3
\(\dfrac{2}{3}\sqrt{x-3}+\dfrac{1}{6}\sqrt{x-3}-\sqrt{x-3}=-\dfrac{2}{3}\)
=>\(\sqrt{x-3}\cdot\left(\dfrac{2}{3}+\dfrac{1}{6}-1\right)=-\dfrac{2}{3}\)
=>\(\sqrt{x-3}\cdot\dfrac{-1}{6}=-\dfrac{2}{3}\)
=>\(\sqrt{x-3}=\dfrac{2}{3}:\dfrac{1}{6}=\dfrac{2}{3}\cdot6=\dfrac{12}{3}=4\)
=>x-3=16
=>x=19(nhận)
NH
1
27 tháng 12 2021
\(\sqrt{x+1}-4x^2=\sqrt{3x}-1\left(x\ge0\right)\left(1\right)\)
\(\Leftrightarrow-4x^2+1+\sqrt{x+1}-\dfrac{\sqrt{6}}{2}=\sqrt{3x}-\dfrac{\sqrt{6}}{2}\)
\(\Leftrightarrow-\left(2x-1\right)\left(2x+1\right)+\dfrac{x+1-\dfrac{3}{2}}{\sqrt{x+1}+\dfrac{\sqrt{6}}{2}}=\dfrac{3x-\dfrac{3}{2}}{\sqrt{3x}+\dfrac{\sqrt{6}}{2}}\)
\(\Leftrightarrow-4\left(x-\dfrac{1}{2}\right)\left(x+\dfrac{1}{2}\right)+\dfrac{x-\dfrac{1}{2}}{\sqrt{x+1}+\dfrac{\sqrt{6}}{2}}-\dfrac{3\left(x-\dfrac{1}{2}\right)}{\sqrt{3x}+\dfrac{\sqrt{6}}{2}}=0\)
\(\Leftrightarrow\left(x-\dfrac{1}{2}\right)\left[-4\left(x+\dfrac{1}{2}\right)+\dfrac{1}{\sqrt{x+1}+\dfrac{\sqrt{6}}{2}}-\dfrac{3}{\sqrt{3x}+\dfrac{\sqrt{6}}{2}}\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\left(tm\right)\\-4\left(x+\dfrac{1}{2}\right)+\dfrac{1}{\sqrt{x+1}+\dfrac{\sqrt{6}}{2}}-\dfrac{3}{\sqrt{3x}+\dfrac{\sqrt{6}}{2}}=0\left(2\right)\end{matrix}\right.\)
\(\left(x\ge0\right)\Rightarrow\left(2\right)< 0\Rightarrow\left(2\right)vô\) \(nghiệm\)
\(\Rightarrow S=\left\{\dfrac{1}{2}\right\}\)
\(\)
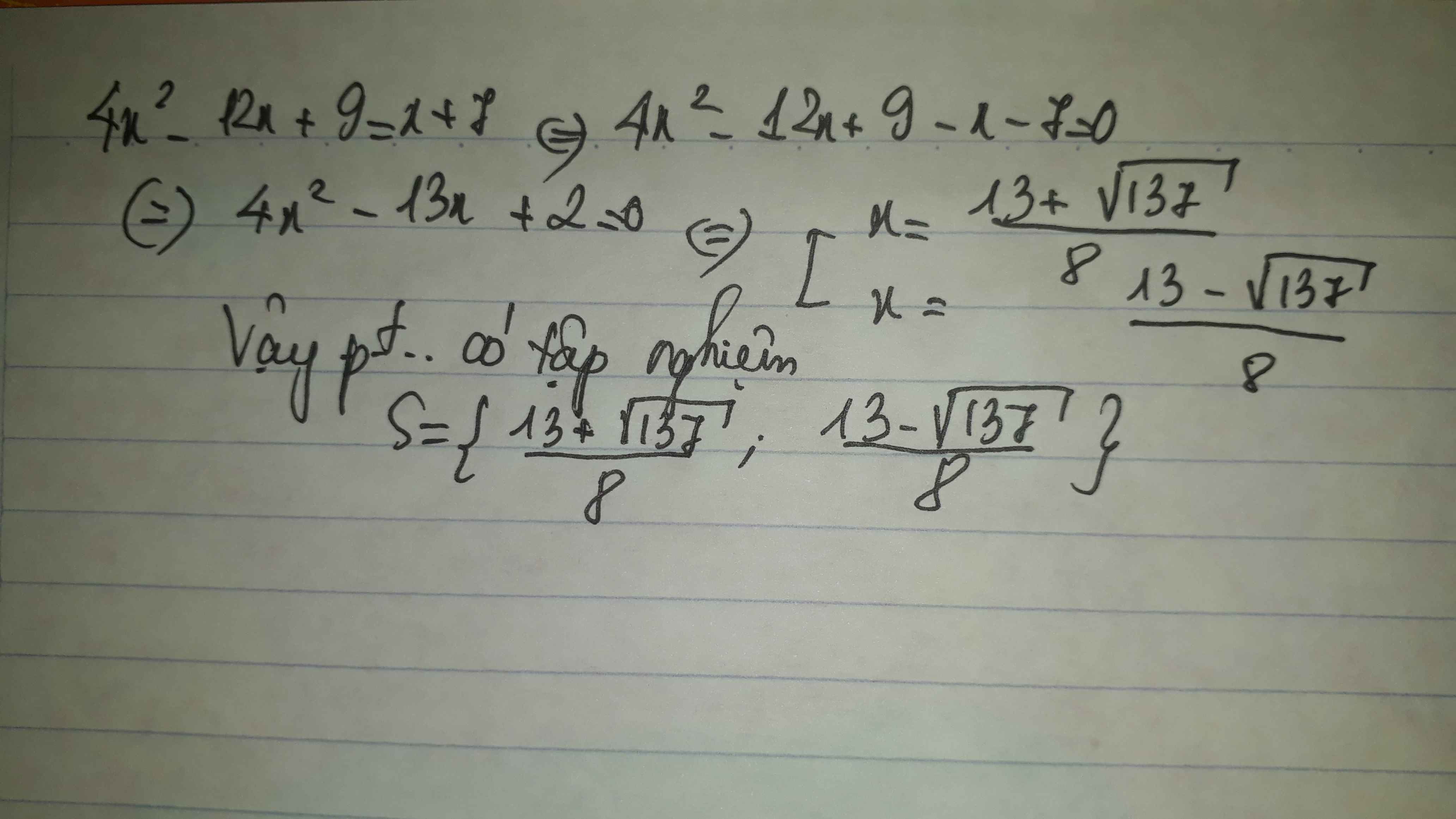
\(4x^2+\sqrt{2x+1}+6=12x\)
Đk:\(x\ge-\frac{1}{2}\)
\(\Leftrightarrow\sqrt{2x+1}=12-4x^2-6\)
Bình phương 2 vế
\(2x+1=16x^4-96x^3+192x^2-144x+36\)
..... thua
số khủng quá mk nản r`