Cho hình thoi ABCD. Trên AB và CD lấy P, Q sao cho AP bằng 1 phần 3 của AB, CQ bằng 1 phần 3 của CD. Gọi I là giao điểm của PQ và AD. Gọi K là giao điểm của DP và BI.CMR:
a) Tam giác BID vuông.
b) BK = IK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 10 2023
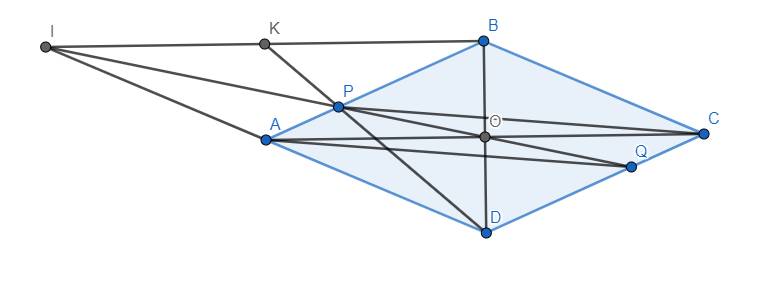
a) ABCD là hình thoi nên AB//CD và \(AB=CD\). Gọi O là giao điểm của AC và BD thì O là trung điểm của AC.
\(\Rightarrow\) AP//CQ và \(AP=\dfrac{1}{3}AB=\dfrac{1}{3}CD=CQ\) nên APCQ là hình bình hành.
Do đó PQ đi qua trung điểm O của AC.
Áp dụng định lý Menelaus cho tam giác BAD, cát tuyến IPO, ta có:
\(\dfrac{IA}{ID}.\dfrac{OD}{OB}.\dfrac{PB}{PA}=1\) \(\Rightarrow\dfrac{IA}{ID}.1.2=1\) \(\Rightarrow\dfrac{IA}{ID}=\dfrac{1}{2}\) hay A là trung điểm ID.
Từ đó dễ thấy IO là đường trung bình của tam giác DIB, suy ra BI//AO. Lại có \(AO\perp BD\) (tính chất hình thoi) nên \(BI\perp BD\), suy ra đpcm.
b) Dễ thấy P là trọng tâm tam giác BID nên K là trung điểm IB hay \(BK=IK\). Ta có đpcm.