Cho tam giác ABC có góc A = 80 độ. Vẽ cung tròn tâm B bán kính = AC, vẽ cung tròn tâm C bán kính = BA. Hai cung tròn này cắt nhau tại M nằm khác của A đối với BC.
a, Tính góc BMC.
b, Chứng minh: CM // AB và BM //AC
(Các bạn làm nhanh hộ mình nha)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TP
29 tháng 11 2021
Tham khảo
ΔΔABC và ΔΔDCB có AB=CD (gt)
BC chung AC=DB (gt)
Vậy ΔΔABC = ΔΔDCB (c.c.c)
Suy ra ˆBDC=ˆA=800BDC^=A^=800 (hai góc tương ứng)
b) Do ΔΔABC = ΔΔDCB (câu a) do đó ˆABC=ˆBCDABC^=BCD^ (hai góc tương ứng của hai tam giác bằng nhau)
Hai góc này ở vị trí so le trong của hai đường thẳng AB và CD cắt đường thẳng BC do đó CD // AB.
11 tháng 11 2016
a)
ta có D là giao điểm của cung tròn tâm B với cung tròn tâm C=>BD là bán kính của cung tròn tâm B và CD là bán kính của cung tròn tâm C
ta có: DB là bán kính của cung tròn tâm B mà AC cũng là bán kính của cung tròn tâm B=> AC=BD
CM tương tự ta có: CD=AB
xét \(\Delta ABC\) và \(\Delta DCB\) có:
BD=AC(cmt)
AB=DC(cmt)
BC(chung)
\(\Rightarrow\Delta ABC=\Delta DCB\left(c.c.c\right)\)
=>\(\widehat{BAC}=\widehat{BDC}=80^o\)
b)
theo câu a, ta có:
\(\Delta ABC=\Delta DCB\Rightarrow\widehat{ABC}=\widehat{BCD}\)
=>CD//AB(2 góc slt)
11 tháng 11 2016
Nếu bạn xem ko đc hình thì xem hình này cũng được, khi nãy mk vẽ quên căn
ở câu a, mk ko quen cách diễn đạt lớp 9 cho lắm nên thông cảm nhé
CM
23 tháng 9 2017
Xét ΔABC và ΔCDA, ta có:
AB = CD (theo cách vẽ)
AC cạnh chung
BC = AD (theo cách vẽ)
Suy ra: ΔABC = ΔCDA (c.c.c) ⇒ ∠(ACB) =∠(CAD) (hai góc tương ứng)
Vậy AD // BC ( vì có cặp góc so le trong bằng nhau)
11 tháng 10 2015
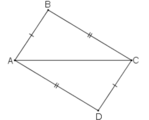
a) D \(\in\) (B; AC) => BD = AC
D \(\in\) (C; AB) => CD = AB
Xét tam giác ABC và DCB có: BC chung; AB = DC; AC = DB
=> tam giác ABC = DCB (c - c- c)
=> góc BAC = CDB (2 góc tương ứng) => góc CDB = 80o
và góc ABC = DCB . Mà 2 góc này ở vị trí so le trong nên AB // CD
mo beeg.com ma coi