Cho hàm số \(y=\dfrac{x-2}{x+1}\) và điểm I(-1;1) . Tìm các tiếp tuyến của đồ thị hàm số biết khoảng cách từ điểm I đến tiếp tuyến đó đạt giá trị lớn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 12 2021
Vì hai đồ thị cắt nhau tại một điểm trên trục tung nên n=-4
=>m=-2
H9
HT.Phong (9A5)
CTVHS
7 tháng 12 2023
a)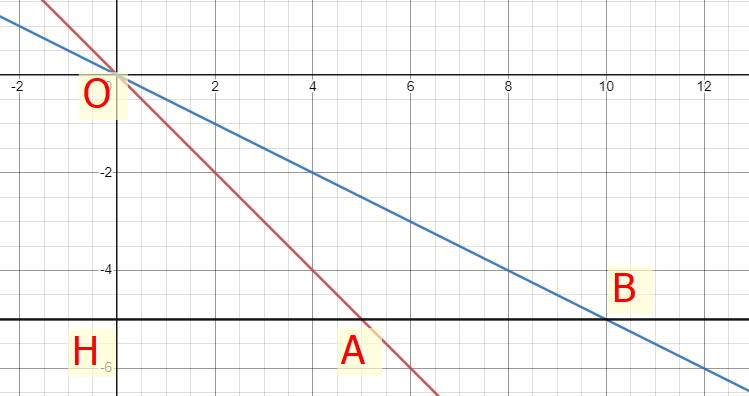 
b) Ta có đường thẳng đi qua điểm H(0;-5) nên phương trình đường thẳng đi qua H là:
\(y=0x-5\Rightarrow y=-5\)
Phương trình hoành độ giao điểm của đường thẳng \(y=-5\) và \(y=-x\) là:
\(-5=-x\)
\(\Rightarrow x=5\)
Tọa độ điểm A là (5;-5)
Phương trình hoành độ giao điểm của đường thẳng \(y=-5\) và \(y=-\dfrac{1}{2}x\) là:
\(-5=-\dfrac{1}{2}x\)
\(\Rightarrow\dfrac{1}{2}x=5\)
\(\Rightarrow x=5:\dfrac{1}{2}\)
\(\Rightarrow x=10\)
Tọa độ điểm B là (10;-5)
c) Ta có: A(5;-5) và B(10;-5)
Độ dài đường thẳng AB là \(10-5=5\left(đvđd\right)\)
Có A(5;-5) ⇒ HA = 5 (đvđd)
Xét tam giác OHA vuông tại H áp dụng định lý Py-ta-go ta có:
\(OA^2=HA^2+OH^2\) (tọa độ điểm H(0;-5) nên OH = 5 đvđd)
\(\Rightarrow OA=\sqrt{5^2+5^2}=\sqrt{50}=5\sqrt{2}\left(đvđd\right)\)
Có B(10;-5) ⇒ HB = 10 (đvđd)
Xét tam giác OHB vuông tại H áp dụng định lý Py-ta-go ta có:
\(OB^2=HB^2+OH^2\)
\(\Rightarrow OB=\sqrt{10^2+5^2}=\sqrt{125}=5\sqrt{5}\left(đvđd\right)\)
Chu vi: \(C_{OAB}=AB+OA+OB=5+5\sqrt{2}+5\sqrt{5}\approx23,25\left(đvđd\right)\)
Diện tích: \(S_{OAB}=\dfrac{1}{2}\cdot OH\cdot AB=\dfrac{1}{2}\cdot5\cdot5=12,5\left(đvdt\right)\)
11 tháng 10 2021
b: Phương trình hoành độ giao điểm là:
\(\dfrac{1}{4}x^2=\dfrac{1}{2}x+2\)
\(\Leftrightarrow x^2-2x-8=0\)
\(\Leftrightarrow\left(x-4\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=\dfrac{1}{4}\cdot4^2=4\\y=\dfrac{1}{4}\cdot\left(-2\right)^2=1\end{matrix}\right.\)
26 tháng 2 2022
a, Hoành độ giao điểm tm pt
\(x^2-\dfrac{1}{2}x=0\Leftrightarrow x\left(x-\dfrac{1}{2}\right)=0\Leftrightarrow x=0;x=\dfrac{1}{2}\)
Với x = 0 => y = 0
Với x = 1/2 => y = 1/4
Vậy (P) cắt (d) tại O(0;0) ; A(1/2;1/4)
17 tháng 9 2023
1) \(y=x^2-3\sqrt[]{x}+\dfrac{1}{x}\)
\(\Rightarrow y=2x-\dfrac{3}{2\sqrt[]{x}}-\dfrac{1}{x^2}\)
2) \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt[]{x}\)
\(\Rightarrow f'\left(x\right)=\dfrac{1.\left(x+3\right)-1\left(x+9\right)}{\left(x+3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{x+3-x-9}{\left(x+3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{-6}{\left(x+3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(1\right)=\dfrac{-6}{\left(1+3\right)^2}+\dfrac{2}{\sqrt[]{1}}=-\dfrac{3}{8}+2=\dfrac{13}{8}\)
N
29 tháng 11 2021
PTHĐGĐ của hai hs:
\(\dfrac{2}{3}x=x^2-x+\dfrac{2}{3}\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{2}{3}\end{matrix}\right.\)
Thay x vào hàm số đầu tiên: \(\left[{}\begin{matrix}y=\dfrac{2}{3}\cdot1=\dfrac{2}{3}\\y=\dfrac{2}{3}\cdot\dfrac{2}{3}=\dfrac{4}{9}\end{matrix}\right.\)
Vậy hai hs cắt nhau tại: \(\left[{}\begin{matrix}A\left(1;\dfrac{2}{3}\right)\\A\left(\dfrac{2}{3};\dfrac{4}{9}\right)\end{matrix}\right.\)
\(y'=\dfrac{3}{\left(x+1\right)^2}\Rightarrow\) phương trình tiếp tuyến tại \(M\left(m;\dfrac{m-2}{m+1}\right)\) có dạng:
\(y=\dfrac{3}{\left(m+1\right)^2}\left(x-m\right)+\dfrac{m-2}{m+1}\)
\(\Leftrightarrow3x-\left(m+1\right)^2y+m^2-4m-2=0\)
\(P=d\left(I;d\right)=\dfrac{\left|6m+6\right|}{\sqrt{9+\left(m+1\right)^4}}=\dfrac{6}{\sqrt{\left(m+1\right)^2+\dfrac{9}{\left(m+1\right)^2}}}\le\dfrac{6}{\sqrt{2\sqrt{\dfrac{9\left(m+1\right)^2}{\left(m+1\right)^2}}}}=\sqrt{6}\)
Dấu "=" xảy ra khi và chỉ khi:
\(\left(m+1\right)^2=\dfrac{9}{\left(m+1\right)^2}\Leftrightarrow\left(m+1\right)^2=3\Rightarrow m=\) ... lại xấu :)