54 : y + 3 = 12
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TG
1
8 tháng 8 2017
a)Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{x}{3}=\frac{y}{7}=\frac{z}{4}=\frac{x+y-z}{3+7-4}=\frac{12}{6}=6\)
+/ \(\frac{x}{3}=6\) => \(x=18\)
+/ \(\frac{y}{7}=6\) => \(y=42\)
+/ \(\frac{z}{4}=6\) => \(z=24\)
b)Ta có: \(\frac{x}{3}=\frac{y}{7}=\frac{z}{y}\) (=) \(\frac{2x}{6}=\frac{3y}{21}=\frac{z}{y}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{2x}{6}=\frac{3y}{21}=\frac{z}{y}=\frac{2x+3y}{6+21}=\frac{54}{27}=2\)
+/ \(\frac{x}{3}=2\) => \(x=6\)
+/ \(\frac{y}{7}=2\) => \(y=14\)
+/ \(\frac{z}{y}=2\) => \(z=2y=2.14=28\)
T i c k nha ^^
CM
3 tháng 4 2019
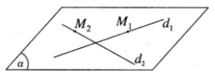
Mặt phẳng ( α ) chứa M 1 và có vecto pháp tuyến là n → , vậy phương trình của ( α ) là:
–2(x – 1) + 16(y + 2) + 13(z – 5) = 0 – 2(x – 1) + 16(y + 2) + 13(z – 5) = 0 hay 2x – 16y – 13z + 31 = 0
7 tháng 1 2017
Câu a cách làm là đúng. Đây là một ví dụ điển hình của phép cộng các phân số cùng mẫu, chỉ là thay dấu phân số thành dấu chia thôi, thực chất không khác chút nào cả.
Tuy nhiên câu b lại là hai phân số không cùng mẫu mà chỉ là cùng tử. Ta không có quy tắc cộng hai phân số cùng tử mà giữ nguyên tử, lại đi cộng mẫu cả. Chỉ có thể rút nhân tử chung ra, quy đồng và tính thôi.
CM
28 tháng 8 2018
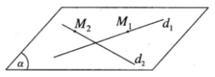
=Ta có ad 1 → = (2; −3; 4) và ad 2 → = (3; 2; −2)
n → = ad 1 → ∧ ad 2 → = (−2; 16; 13)
Lấy điểm M 1 (1; -2; 5) trên d 1 và điểm M 2 (7; 2; 1) trên d 2 .
Ta có M 1 M 2 → = (6; 4; −4)
n → . M 1 M 2 → = −12 + 64 – 52 = 0
Suy ra d 1 và d 2 cùng nằm trong mặt phẳng ( α )
CM
11 tháng 2 2018
Chọn A
Từ hệ gồm phương trình đường thẳng d và mặt phẳng (P) ta tìm được điểm A. Mặt cầu có tâm I và bán kính R = IA.
KS
0
54 : y + 3 = 12
54 : y = 12 - 3
54 : y = 9
y = 54 : 9
y = 6
54 : y + 3 = 12
54 : y = 12 - 3
54 : y = 9
y = 54 : 9
y = 6