cho tam giác ABC vuông tại A vẽ AH vuông với BC tại H vẽ AX là tia đối của tia AC
CMR a, góc ABH=C
b, góc XAH và B bù nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
16 tháng 12 2023
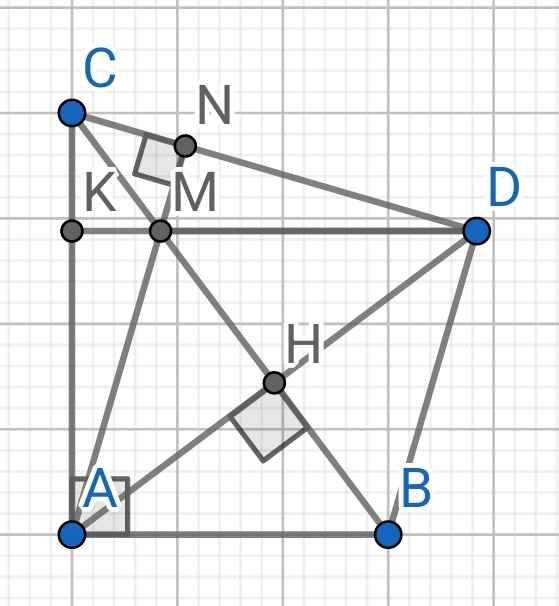a) Sửa đề: Chứng minh ABH = DBH
Giải:
Xét hai tam giác vuông: ∆ABH và ∆DBH có:
BH là cạnh chung
AH = DH (gt)
⇒ ∆ABH = ∆DBH (hai cạnh góc vuông)
⇒ ∠ABH = ∠DBH (hai góc tương ứng)
⇒ BH là tia phân giác của ∠ABD
b) Do DM // AB (gt)
⇒ ∠MDH = ∠HAB (so le trong) (1)
Do ∆ABH = ∆DBH (cmt)
⇒ ∠HAB = ∠HDB (hai góc tương ứng) (2)
Từ (1) và (2) ⇒ ∠MDH = ∠HDB
Xét hai tam giác vuông: ∆DHM và ∆DHB có:
DH là cạnh chung
∠MDH = ∠HDB (cmt)
⇒ ∆DHM = ∆DHB (cạnh góc vuông - góc nhọn kề)
⇒ ∠DHM = ∠DHB (hai góc tương ứng)
Mà ∠DHM + ∠DHB = 180⁰ (kề bù)
⇒ ∠DHM = ∠DHB = 180⁰ : 2 = 90⁰
⇒ DH ⊥ BM (3)
Do ∆DHM = ∆DHB (cmt)
⇒ HM = HB
⇒ H là trung điểm của BM (4)
Từ (3) và (4) ⇒ HD là đường trung trực của BM
⇒ AD là đường trung trực của BM
c) Do AD là đường trung trực của BM (cmt)
⇒ AD ⊥ CH
Do DK // AB (gt)
⇒ DK ⊥ AC (AB ⊥ AC)
∆ACD có:
CH là đường cao (CH ⊥ AD)
DK là đường cao thứ hai (DK ⊥ AC)
⇒ AM là đường cao thứ ba
Mà AM ⊥ CN tại N
⇒ AN là đường cao thứ ba của ∆ACD
⇒ C, N, D thẳng hàng
21 tháng 12 2022
a: Xét ΔABH vuông tại H và ΔDBH vuông tại H có
BH chung
HA=HD
Do đó: ΔABH=ΔDBH
b: Xét ΔABC và ΔDBC có
BA=BD
góc ABC=góc DBC
BC chung
Do đó: ΔABC=ΔDBC
=>góc BDC=90 độ
c: ΔABC=ΔDBC
nên góc ACB=góc DCB
=>CB là phân giác của góc ACD
LQ
29 tháng 12 2022
a) vì tam giác ABC cân tại A nên góc B = góc C = 65độ(2 góc tương ứng )
ta có : gócA + gócB + gócC = 180độ( tổng 3 góc 1 tam giác )
gócA + 65độ + 65độ = 180độ
=>gócA = 180 - 65 - 65 =50
b)xét tam giác ABH và tam giác ACH , có :
gócB = gócC
AB = AC
=>tam giác ABH = tam giác ACH (cạnh huyền - góc nhọn )
câu c tui ko biết làm
23 tháng 3 2016
1.
Ta có : AC<AD (vì : D là tia đối của tia BC )
=> HD<HC
3.
Ta có : AB+AC>AH (vì : tog 2 cah cua tam giác luôn lớn hơn cah con lại)
Mà : 1/2AH<AB+AC
=> AB+AC>2AH
4.
Ta có : ko hiu
Trả lời nhanh hộ mình với mình đang vội
nhanh lên mình đang vội