tìm a thuộc Z để (a2-1)(a2-4)(a2-7)(a2-10) <0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bạn đã k đủ 3k hẹn lần sau
Bai 1. tinh chat bac cau
bai 2> a) x=+-2003
b) >x=0
c)x=y=0



Ta có:
\(\dfrac{1}{a+b}+\dfrac{1}{b+c}\ge\dfrac{4}{a+2b+c}\ge\dfrac{4}{\dfrac{a^2+1}{2}+b^2+1+\dfrac{c^2+1}{2}}=\dfrac{8}{b^2+7}\)
Tương tự
\(\dfrac{1}{a+b}+\dfrac{1}{a+c}\ge\dfrac{8}{a^2+7}\)
\(\dfrac{1}{b+c}+\dfrac{1}{a+c}\ge\dfrac{8}{c^2+7}\)
Cộng vế:
\(2\left(\dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{c+a}\right)\ge\dfrac{8}{a^2+7}+\dfrac{8}{b^2+7}+\dfrac{8}{c^2+7}\)
\(\Rightarrow\dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{c+a}\ge\dfrac{4}{a^2+7}+\dfrac{4}{b^2+7}+\dfrac{4}{c^2+7}\)
Dấu "=" xảy ra khi \(a=b=c=1\)

\(\Leftrightarrow49< a^2< 81\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}a>7\\a< -7\end{matrix}\right.\\-9< a< 9\end{matrix}\right.\)

Điều kiện x ≠ 2 và x ≠ 0
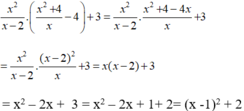
Vì x - 1 2 ≥ 0 nên x - 1 2 + 2 ≥ 2 với mọi giá trị của x.
Khi đó giá trị nhỏ nhất của biểu thức bằng 2 khi x = 1.
Vậy biểu thức đã cho có giá trị nhỏ nhất bằng 2 tại x = 1.

chon dai di thoi
a1=1
a2=3
=>d3=2
d1=a1-a3 de sai roi a1<a3 khong co d1

Điều kiện x ≠ -2 và x ≠ 0
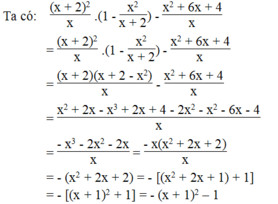
Vì x + 1 2 ≥ 0 nên - x + 1 2 ≤ 0 ⇒ - x + 1 2 - 1 ≤ - 1
Khi đó biểu thức có giá trị lớn nhất bằng -1 khi x = -1
Vậy biểu thức đã cho có giá trị lớn nhất bằng -1 tại x = -1.
Vì tích (a2 -1)(a2 - 4)(a2 - 7)(a2 - 10) là tích của 4 thừa số nhỏ hơn 0
=> Có 1 hoặc 3 thừa số nhỏ hơn 0
Mà a2 - 1 > a2 - 4 > a2 - 7 > a2 - 10.
TH1 : Có 1 thừa số nguyên âm
=> a2 - 7 > 0 => a2 > 7
=> a2 - 10 < 0 => a2 < 10
=> 7< a2< 10 => a2 = 9 => a ∈{ 3; -3}
TH2 : Có 3 thừa số nguyên âm
=> a2 - 1 > 0 => a2 > 1
=> a2 - 4 < 0 => a2 < 4
=> 1< a2 < 4 => a2 \(\in\) ∅ => a \(\in\)∅
Vậy a ∈{3 ; -3}
vì ( \(a^2-1\))\(\left(a^2-4\right)\left(a^2-7\right)\left(a^2-10\right)\) là tích của 4 thừa số nhỏ hơn 0
=> có 1 hoặc 3 số nhỏ hơn 0
mà \(a^2-1>a^2-4>a^2-7>a^2-10\)
TH1 : có 1 thừa số nguyên âm
=> \(a^2-7>0=>a^2>7\)
=> \(a^2-10<0=>a^2<10\)
=> 7 < \(a^2\) < 10 => \(a^2=9\) => a= 3 hoặc a = -3
TH2 có 3 thừa số nguyên âm
=>\(a^2-1>0=>a^2>1\)
=>\(a^2-4<0=>a^2<4\)
=> 1 < \(a^2\) <4 => \(a^2\) thuộc rỗng => a thuộc rỗng
vậy a= 3 hoặc a=-3