Chứng minh đẳng thức \(\sqrt{\left(\sqrt{5}-4\right)^2}-\sqrt{5}+\sqrt{20}=4\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(VT=\left(\dfrac{\sqrt{14.14}}{\sqrt{14}}+\dfrac{\sqrt{6}\left(\sqrt{2}+\sqrt{5}\right)}{\sqrt{2}+\sqrt{5}}\right).\sqrt{5-\sqrt{21}}\)
\(=\left(\sqrt{14}+\sqrt{6}\right)\sqrt{5-\sqrt{21}}\)
\(=\sqrt{30-6\sqrt{21}}+\sqrt{70-14\sqrt{21}}\)
\(=\sqrt{21-2.3\sqrt{21}+9}+\sqrt{21-2.7.\sqrt{21}+49}\)
\(=\sqrt{\left(\sqrt{21}-3\right)^2}+\sqrt{\left(7-\sqrt{21}\right)^2}\)
\(=\sqrt{21}-3+7-\sqrt{21}=4\)

\(\left(4-\sqrt{7}\right)^2=4^2-2\cdot4\cdot\sqrt{7}+7\)
\(=16-8\sqrt{7}+7=23-8\sqrt{7}\)
\(\sqrt{9-4\sqrt{5}}-\sqrt{5}\)
\(=\sqrt{5-2\cdot\sqrt{5}\cdot2+4}-\sqrt{5}\)
\(=\sqrt{\left(\sqrt{5}-2\right)^2}-\sqrt{5}\)
\(=\left|\sqrt{5}-2\right|-\sqrt{5}\)
\(=\sqrt{5}-2-\sqrt{5}=-2\)
\(\dfrac{\sqrt{4-2\sqrt{3}}}{1+\sqrt{2}}:\dfrac{\sqrt{2}-1}{\sqrt{3}+1}\)
\(=\dfrac{\sqrt{3-2\cdot\sqrt{3}\cdot1+1}}{\sqrt{2}+1}\cdot\dfrac{\sqrt{3}+1}{\sqrt{2}-1}\)
\(=\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{\sqrt{2}+1}\cdot\dfrac{\sqrt{3}+1}{\sqrt{2}-1}\)
\(=\dfrac{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}=\dfrac{3-1}{2-1}=2\)
\(\left(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\left(\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}-\dfrac{6\sqrt{6}}{3}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\left(\dfrac{1}{2}\sqrt{6}-2\sqrt{6}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\dfrac{1}{2}-2=-\dfrac{3}{2}=-1,5\)

\(=\left(\dfrac{\sqrt{10}\left(\sqrt{3}-\sqrt{2}\right)}{\sqrt{3}-\sqrt{2}}-\dfrac{\sqrt{6^2}}{\sqrt{6}}\right)\sqrt{4+\sqrt{15}}\)
\(=\sqrt{2}\left(\sqrt{5}-\sqrt{3}\right)\sqrt{4+\sqrt{15}}\)
\(=\left(\sqrt{5}-\sqrt{3}\right)\sqrt{5+2\sqrt{3}\sqrt{5}+3}\)
\(=\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)=5-3=2\)
\(VT\Leftrightarrow\left(\sqrt{10}-\sqrt{6}\right)\sqrt{4+\sqrt{15}}=\left(\sqrt{5}-\sqrt{3}\right)\sqrt{8+2\sqrt{15}}=\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)=5-3=2=VP\left(dpcm\right)\)

Ta có VT: \(\sqrt{\frac{4}{\left(2-\sqrt{5}\right)^2}}-\sqrt{\frac{4}{\left(2+\sqrt{5}\right)^2}}\)=\(\frac{\sqrt{4}}{\sqrt{\left(2-\sqrt{5}\right)^2}}-\frac{\sqrt{4}}{\sqrt{\left(2+\sqrt{5}\right)^2}}\)
=\(\frac{2}{\left|2-\sqrt{5}\right|}-\frac{2}{\left|2+\sqrt{5}\right|}\)
=\(\frac{2}{\sqrt{5}-2}-\frac{2}{2+\sqrt{5}}\)
=\(\frac{2.\left(2+\sqrt{5}\right)-2.\left(\sqrt{5}-2\right)}{\left(\sqrt{5}-2\right).\left(2+\sqrt{5}\right)}\)
=\(2.\left(2+\sqrt{5}\right)-2.\left(\sqrt{5}-2\right)\)
=\(4+2\sqrt{5}-2\sqrt{5}+4\)
=8 (bằng VP)

a, \(\sqrt{\left(\sqrt{5}-4\right)^2}-\sqrt{5}+\sqrt{20}=4\)
\(VT=\sqrt{\left(4-\sqrt{5}\right)^2}-\sqrt{5}+\sqrt{20}=\left|4-\sqrt{5}\right|-\sqrt{5}+\sqrt{20}\)
\(=4-\sqrt{5}-\sqrt{5}+2\sqrt{5}=4\) hay \(VT=VP\)
Vậy ta có đpcm
b, Với \(x>0,x\ne4\)
\(P=\left(\frac{1}{\sqrt{x}+2}+\frac{1}{\sqrt{x}-2}\right):\frac{2}{x-2\sqrt{x}}\)
\(=\left(\frac{\sqrt{x}-2+\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\right):\frac{2}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\frac{2\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}.\frac{\sqrt{x}\left(\sqrt{x}-2\right)}{2}=\frac{x}{\sqrt{x}+2}\)
1.
Giả sử điều trên là đúng ta có:
\( \left | \sqrt{5}-4 \right |-\sqrt{5}+\sqrt{20}=4\)
Ta có: \(4>\sqrt{5}\)
\(\Rightarrow 4-\sqrt{5}- \sqrt{5}+\sqrt{20}=4\)
\(\Leftrightarrow 4-\sqrt{20}+\sqrt{20}=4\)
\(\Rightarrow đpcm\)
2.
chứng minh đẳng thức:\(\left(4+\sqrt{15}\right).\left(\sqrt{10}\sqrt{6}\right)\sqrt{4-\sqrt{15}=2}\)

Lời giải:
$(4+\sqrt{15})(\sqrt{10}-\sqrt{6})\sqrt{4-\sqrt{15}}$
$=(4+\sqrt{15})(\sqrt{5}-\sqrt{3})\sqrt{8-2\sqrt{15}}$
$=(4+\sqrt{15})(\sqrt{5}-\sqrt{3})\sqrt{(\sqrt{5}-\sqrt{3})^2}$
$=(4+\sqrt{15})(\sqrt{5}-\sqrt{3})(\sqrt{5}-\sqrt{3})$
$=(4+\sqrt{15})(8-2\sqrt{15})=2(4+\sqrt{15})(4-\sqrt{15})$
$=2(4^2-15)=2$ (đpcm)
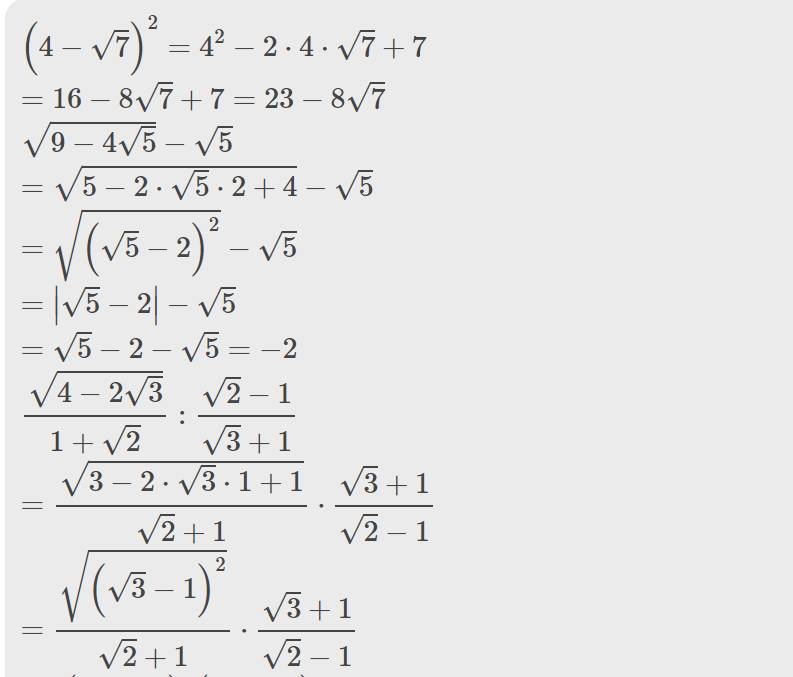
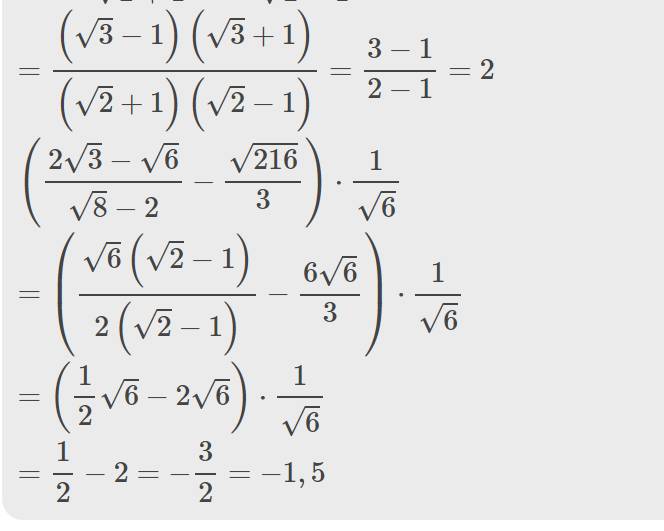

Ta có:
`VT=|\sqrt{5}-4|-\sqrt{5}+\sqrt{2^2 .5}`
`=4-\sqrt{5}-\sqrt{5}+2\sqrt{5}` (Vì `\sqrt{5} < 4`)
`=4=VP`
`=>` Đẳng thức được c/m