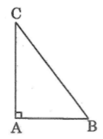
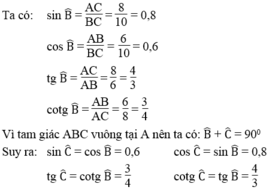Cho tam giac ABC vuông tại B=0,6.tính các tỉ số lượng giác của góc c
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NA
0
SD
0
LK
1
PD
8 tháng 8 2021
Xét $\Delta ABC$:
$\cos B=\sin C=0,6$
$\cos^2B=0,6.0,6=0,36$
Mà $\cos^2B+\sin^2B=1$
$\Rightarrow \sin^2B=0,64\\\Leftrightarrow \sinB=0,8(vì\,\,\sinB>0)$
$\Rightarrow \sin B=\cos C=0,8$
Ta có: $\tan C=\dfrac{\sin C}{\cos C}=\dfrac{0,6}{0,8}=0,75$
$\cotC=\dfrac{\cosC}{\sinC}=\dfrac{0,8}{0,6}=\dfrac{4}{3}$
Vậy $\sin C=0,6;\cos C=0,8;\tanC=0,75;\cotC=\dfrac{4}{3}$
26 tháng 10 2021
\(\cos\widehat{B}=0.6\)
\(\sin\widehat{B}=0.8\)
\(\tan\widehat{B}=\dfrac{4}{3}\)
\(\cot\widehat{B}=\dfrac{3}{4}\)
CD
0
QH
2
22 tháng 7 2023
\(ab=8;ac=15\)
\(\Rightarrow\dfrac{b}{c}=\dfrac{8}{15}\)
\(tanB=\dfrac{b}{c}=\dfrac{8}{15}\Rightarrow cotB=\dfrac{1}{tanB}=\dfrac{15}{8}\left(tanB.cotB=1\right)\)
\(1+tan^2B=\dfrac{1}{cos^2B}\Rightarrow cos^2B=\dfrac{1}{1+tan^2B}\)
\(\Rightarrow cos^2B=\dfrac{1}{1+\dfrac{64}{225}}\dfrac{1}{\dfrac{289}{225}}=\dfrac{225}{289}\)
\(\Rightarrow cosB=\sqrt[]{\dfrac{225}{289}}=\dfrac{15}{17}\)
\(tanB=\dfrac{sinB}{cosB}\Rightarrow sinB=tanB.cosC=\dfrac{8}{15}.\dfrac{15}{17}\)
\(\Rightarrow sinB=\dfrac{8}{17}\)
Vì \(B+C=90^o\Rightarrow C=90^o-B\)
\(\Rightarrow\left\{{}\begin{matrix}sinC=cosB=\dfrac{15}{17}\\cosC=sinB=\dfrac{8}{17}\\tanC=cotB=\dfrac{15}{8}\\cotC=tanB=\dfrac{8}{15}\end{matrix}\right.\)
22 tháng 7 2023
Để tính các tỉ số lượng giác của góc B, ta sử dụng định nghĩa của các tỉ số lượng giác: sin(B) = cạnh đối diện / cạnh huyền = AC / AB = 15 / 8 cos(B) = cạnh kề / cạnh huyền = BC / AB = ? tan(B) = cạnh đối diện / cạnh kề = AC / BC = ? Để tính tỉ số lượng giác của góc C, ta sử dụng định nghĩa của các tỉ số lượng giác: sin(C) = cạnh đối diện / cạnh huyền = AB / AC = 8 / 15 cos(C) = cạnh kề / cạnh huyền = BC / AC = ? tan(C) = cạnh đối diện / cạnh kề = AB / BC = ? Tuy nhiên, để tính các tỉ số lượng giác của góc C, ta cần tìm giá trị của cạnh BC. Ta có thể sử dụng định lý Pythagoras trong tam giác vuông để tìm giá trị này: BC^2 = AC^2 - AB^2 BC^2 = 15^2 - 8^2 BC^2 = 225 - 64 BC^2 = 161 BC = √161 Sau đó, ta có thể tính các tỉ số lượng giác của góc B và góc C: sin(B) = 15 / 8 cos(B) = BC / AB = √161 / 8 tan(B) = 15 / √161 sin(C) = 8 / 15 cos(C) = BC / AC = √161 / 15 tan(C) = 8 / √161
CM
12 tháng 8 2017
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
B C 2 = A B 2 + A C 2 = 6 2 + 8 2 = 100
Suy ra: BC = 10 (cm)
