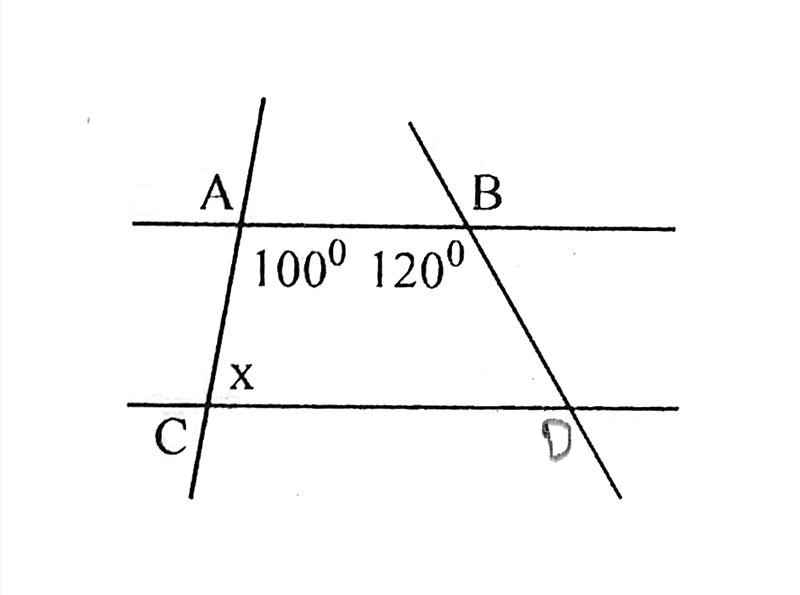
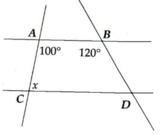
Tìm \(x\) trong hình vẽ dưới đây:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: a//b
nên \(2x+3x=180^0\)
\(\Leftrightarrow5x=180^0\)
hay \(x=36^0\)

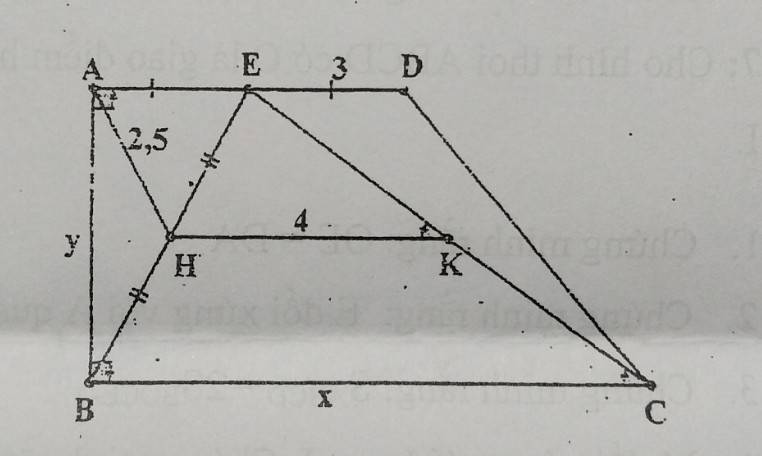
Có: ∠EKH = ∠KCB
Mà 2 góc ở vị trí đồng vị
⇒ HK // BC
Xét △EBC có:
H trung điểm EB
HK // BC
⇒ HK đường trung bình
⇒ HK = \(\dfrac{1}{2}\)BC
⇒ BC = 2HK
⇒ x = 2 . 4 = 8
Xét △AEB ⊥ A, có:
AH đường trung tuyến (H trung điểm EB)
⇒ AH = \(\dfrac{1}{2}\)EB
⇒ EB = 2AH = 2 . 2,5 = 5
Vì AE = ED
Mà ED = 3
⇒ AE = 3
Áp dụng định lý Pytago vào △AEB ⊥ A
⇒ \(EB^2=AE^2+AB^2\)
⇒ AB = y = \(\sqrt{BE^2-AE^2}\) = \(\sqrt{5^2-3^2}\) = \(4\)
Vậy x = 8 và y = 4

Áp dụng định lí Pytago trong tam giác vuông IAD ta có:
A I 2 + A D 2 = I D 2 ⇔ 4 2 + 3 2 = I D 2 ⇔ I D 2 = 25 ⇒ I D = 5
Xét 2 tam giác vuông IAD và CBI có: I D A ^ = C I B ^ (gt)
=> ΔIAD ~ ΔCBI (g - g)
⇒ I A C B = I D C I ⇔ 4 15 = 5 y ⇔ y = 15.5 4 = 18 , 75
Vậy y = 18,75.
Đáp án: C

Lời giải:
Vì $AB\parallel CD$ nên $100^0+x=180^0$ (hai góc trong cùng phía)
$x=180^0-100^0=80^0$

Áp dụng tính chất hai đường thẳng song song ta tính được x = 80 °

Áp dụng tính chất hai đường thẳng song song ta tính được x = 80°
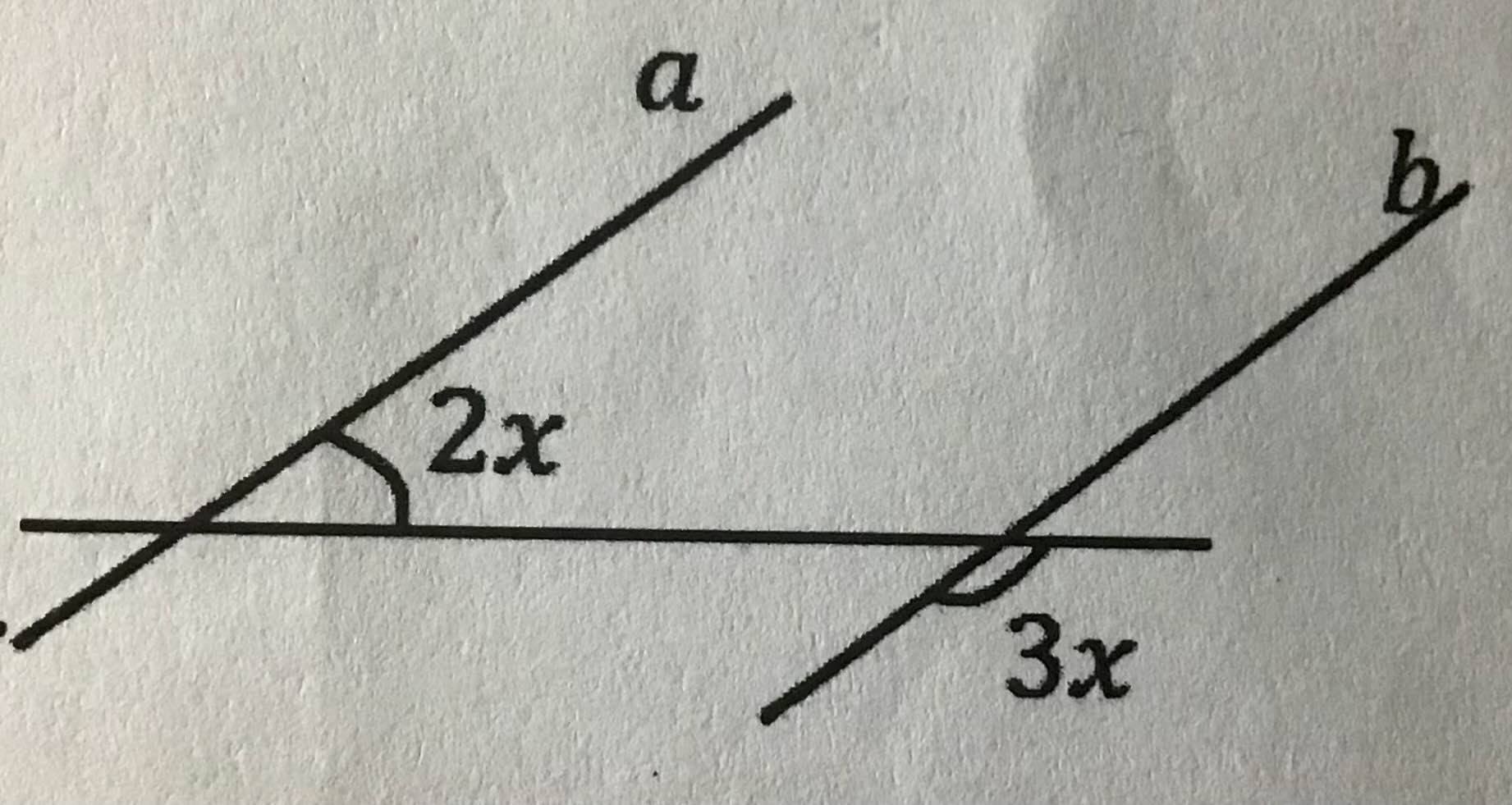



\(\sin\widehat{B}=\dfrac{AC}{BC}\Rightarrow BC=\dfrac{AC}{\sin\widehat{B}}=\dfrac{4}{\sin42^o}\)
\(AC^2=CH.BC\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow CH=\dfrac{AC^2}{BC}=4.\sin42^o\)
Xét tg vuông AHC có
\(x=AH=\sqrt{AC^2-CH^2}\) (Pitago)
\(\Rightarrow x=\sqrt{16-16\sin^242^o}=4\sqrt{1-\sin^242}=4\sqrt{\cos^242^o}=4\cos42^o\)