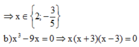Tìm x thuộc R biết x3 -3x + 1 =0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`P(x)=\(4x^2+x^3-2x+3-x-x^3+3x-2x^2\)
`= (x^3-x^3)+(4x^2-2x^2)+(-2x-x+3x)+3`
`= 2x^2+3`
`Q(x)=`\(3x^2-3x+2-x^3+2x-x^2\)
`= -x^3+(3x^2-x^2)+(-3x+2x)+2`
`= -x^3+2x^2-x+2`
`P(x)-Q(x)-R(x)=0`
`-> P(X)-Q(x)=R(x)`
`-> R(x)=P(x)-Q(x)`
`-> R(x)=(2x^2+3)-(-x^3+2x^2-x+2)`
`-> R(x)=2x^2+3+x^3-2x^2+x-2`
`= x^3+(2x^2-2x^2)+x+(3-2)`
`= x^3+x+1`
`@`\(\text{dn inactive.}\)
a: P(x)-Q(x)-R(x)=0
=>R(x)=P(x)-Q(x)
=2x^2+3+x^3-2x^2+x-2
=x^3+x+1

Ta có
x 3 + 3 x 2 + 3 x + 1 = 0 ⇔ ( x + 1 ) 3 = 0
ó x + 1 = 0 ó x = -1
Vậy x = -1
Đáp án cần chọn là: A

a: \(\Leftrightarrow x\left(x-5\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=5\\x=-5\end{matrix}\right.\)



x3 - 3x = 0
x.x2 - 3x = 0
x.(x2 - 3) = 0
=> x = 0 hoặc x2 - 3 = 0
=> x = 0 hoặc x2 = 3
=> x = 0 hoặc x = √3

a) \(\Rightarrow x\left(x+3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=-3\end{matrix}\right.\)
b) \(\Rightarrow x\left(x^2-4\right)=0\Rightarrow x\left(x-2\right)\left(x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)
c) \(\Rightarrow\left(x-1\right)\left(5x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{5}\end{matrix}\right.\)
d) \(\Rightarrow2\left(x+5\right)-x\left(x+5\right)=0\Rightarrow\left(x+5\right)\left(2-x\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-5\\x=2\end{matrix}\right.\)
e) \(\Rightarrow2x^2-10x-3x-2x^2=26\)
\(\Rightarrow-13x=26\Rightarrow x=-2\)
f) \(\Rightarrow\left(x-2012\right)\left(5x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2012\\x=\dfrac{1}{5}\end{matrix}\right.\)