Chỉ cần giải giúp em câu c,d thui ạ
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. playing
2. listening
3. getting
4. seeing
7. exceeding
9. reading
10. stepping
11. be
12. to contact
13. to lose
14. to hear
15. phoning/going
16. Lying/sitting
19. to help/to choose
20. to learn/ listening

b: Thay x=-1 và y=-3 vào (d1), ta được:
-3=-1+2
=>-3=1(loại)
=>A ko thuộc (d1)
Thay x=-1 và y=1 vào (d1), ta đc:
-1+2=1
=>1=1
=>B thuộc (d1)
c: Tọa độ C là:
x+2=-1/2x+2 và y=x+2
=>x=0 và y=2

Câu 1:
1:
a: \(\dfrac{1}{2}x-3=0\)
=>\(\dfrac{1}{2}x=3\)
=>\(x=3:\dfrac{1}{2}=3\cdot2=6\)
b: \(3x^2-12x=0\)
=>\(3x\cdot x-3x\cdot4=0\)
=>\(3x\left(x-4\right)=0\)
=>x(x-4)=0
=>\(\left[{}\begin{matrix}x=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
2:
a: Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2=-x+\dfrac{3}{2}\)
=>\(x^2=-2x+3\)
=>\(x^2+2x-3=0\)
=>(x+3)(x-1)=0
=>\(\left[{}\begin{matrix}x+3=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=1\end{matrix}\right.\)
Khi x=-3 thì \(y=\dfrac{1}{2}\cdot\left(-3\right)^2=\dfrac{1}{2}\cdot9=4,5\)
Khi x=1 thì \(y=\dfrac{1}{2}\cdot1^2=\dfrac{1}{2}\)
b: Gọi (d1): y=ax+b(a<>0) là phương trình đường thẳng cần tìm
Thay x=2 và y=2 vào (d), ta được:
\(a\cdot2+b=2\)
=>2a+b=2
=>b=2-2a
=>y=ax+2-2a
Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2=ax+2-2a\)
=>\(\dfrac{1}{2}x^2-ax-2+2a=0\)
\(\text{Δ}=\left(-a\right)^2-4\cdot\dfrac{1}{2}\cdot\left(2a-2\right)\)
\(=a^2-2\left(2a-2\right)=a^2-4a+4=\left(a-2\right)^2\)
Để (P) tiếp xúc với (d1) thì Δ=0
=>a-2=0
=>a=2
=>b=2-2a=2-4=-2
Vậy: Phương trình đường thẳng cần tìm là y=2x-2

a: \(A=\dfrac{\left(x^2-2x+5\right)\left(x-3\right)}{3\left(x-3\right)}=\dfrac{x^2-2x+5}{3}\)

Bài 7:
a: \(=2006\cdot\left(430-430\right)+100=100\)
b: \(=54\left(7+9-5-1\right)=54\cdot10=540\)



 các bạn giúp mình câu 5 nhé mình cần gấp lắm ạ!!! chỉ trong tối nay thui ạ !!! cảm ơn
các bạn giúp mình câu 5 nhé mình cần gấp lắm ạ!!! chỉ trong tối nay thui ạ !!! cảm ơn 

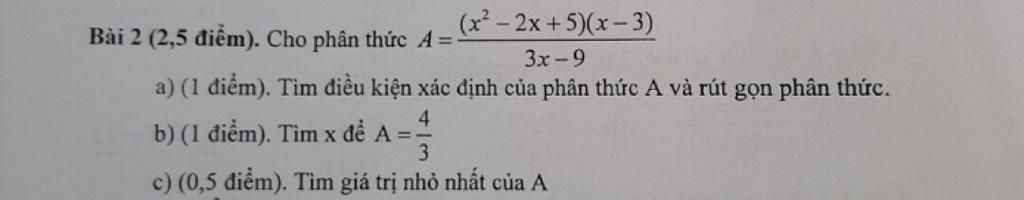

a: Xét ΔEAB có \(\widehat{EBA}=\widehat{EAB}\)
nên ΔEAB cân tại E
mà EK là đường cao
nen K là trung điểm của AB
hay KA=KB
b: Xét ΔACE vuông tại C và ΔBDE vuông tại D có
EA=EB
\(\widehat{AEC}=\widehat{BED}\)
Do đó: ΔACE=ΔBDE
Suy ra: EC=ED
Ta có: AE+ED=AD
BE+CE=BC
mà AE=BE
và ED=EC
nên AD=BC