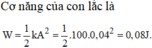Một con lắc lò xo nằm ngang dao động điều hòa với phương trình x = 5cos (10πt + π/3)cm. Chiều dài tự nhiên của lò xo là 20 cm Tính lực đàn hồi cực đại và cực tiểu của lò xo biết khối lượng vật nặng là 100 g lấy π²= 10
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
24 tháng 5 2022
\(l_{max}=l_0+\Delta l+A\Rightarrow\left\{{}\begin{matrix}A=5cm=0,02m\\\Delta l=\dfrac{g}{\omega^2}=\dfrac{10}{\left(10\right)^2}=0,1m\\l_0=0,2m\end{matrix}\right.\)
=> \(l_{max}=0,2+0,1+0,02=0,32\left(m\right)=32cm\)
\(l_{min}=l_0+\Delta l-A=0,2+0,1-0,02=0,28\left(m\right)=28\left(cm\right)\)
Vậy ...
VT
1 tháng 12 2019
Đáp án A
Khi lò xo có chiều dài 18 cm thì vận tốc của vật bằng 0 → vị trí biên trên
→ Độ cứng của lò xo k = F Δ l = 2 0 , 2 − 0 , 18 = 100 N/m
→ Độ biến dạng của lò xo tại vị trí cân bằng Δ l 0 = m g k = 0 , 2.10 100 = 2 cm → A = 4 cm.
Năng lượng dao động E = 0 , 5 k A 2 = 0 , 08 J .
VT
24 tháng 11 2018
Đáp án C
Phương pháp: Áp dụng đại cương dao động điều hòa cho con lắc lò xo đứng
Cách giải:
Chiều dài tự nhiên của lò xo là l 0 = 20 cm
Khi lò xo có chiều dài 18 cm thì vận tốc của vật bằng 0 => khi đó vật đang ở vị trí biên trên :
