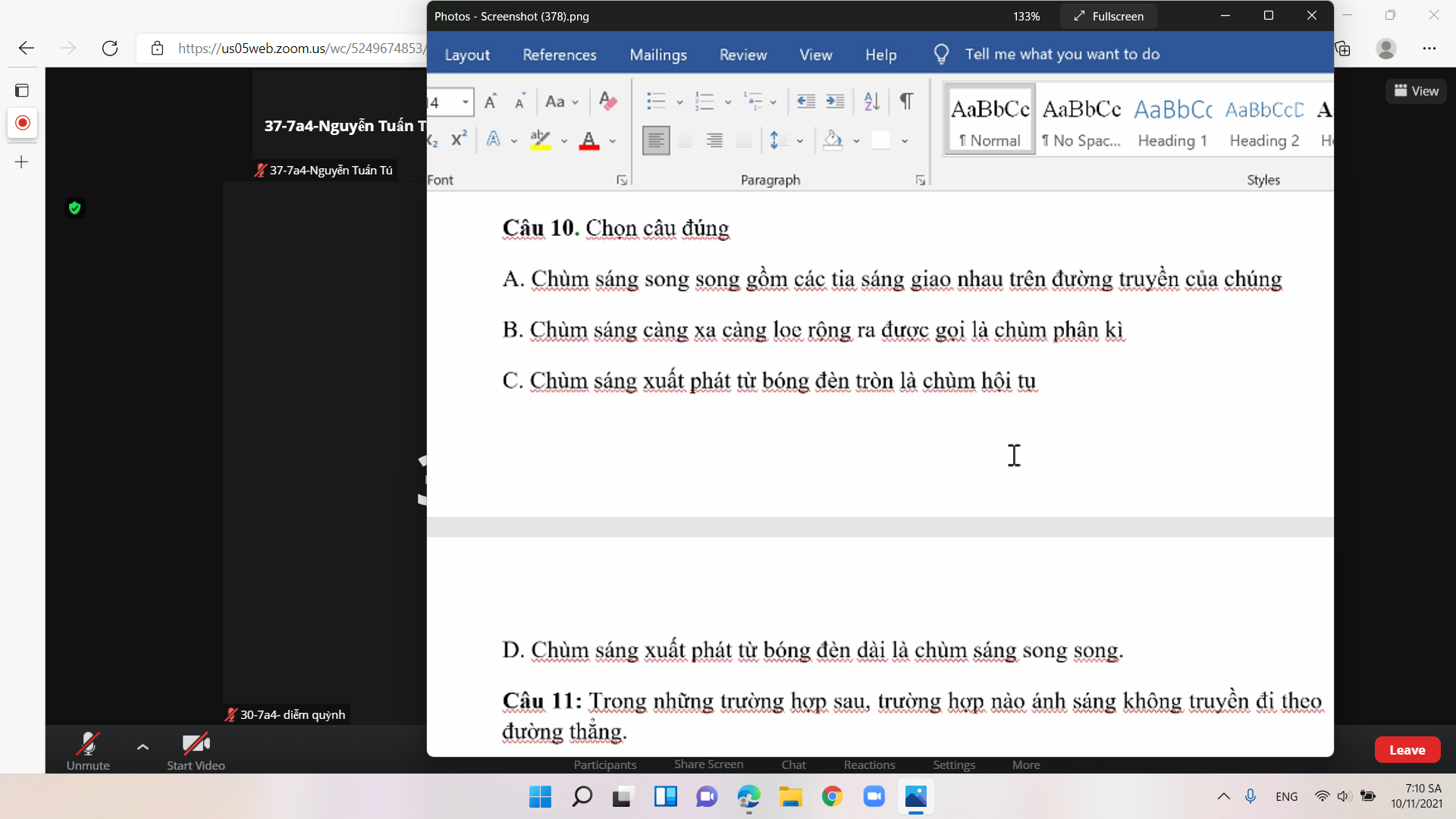
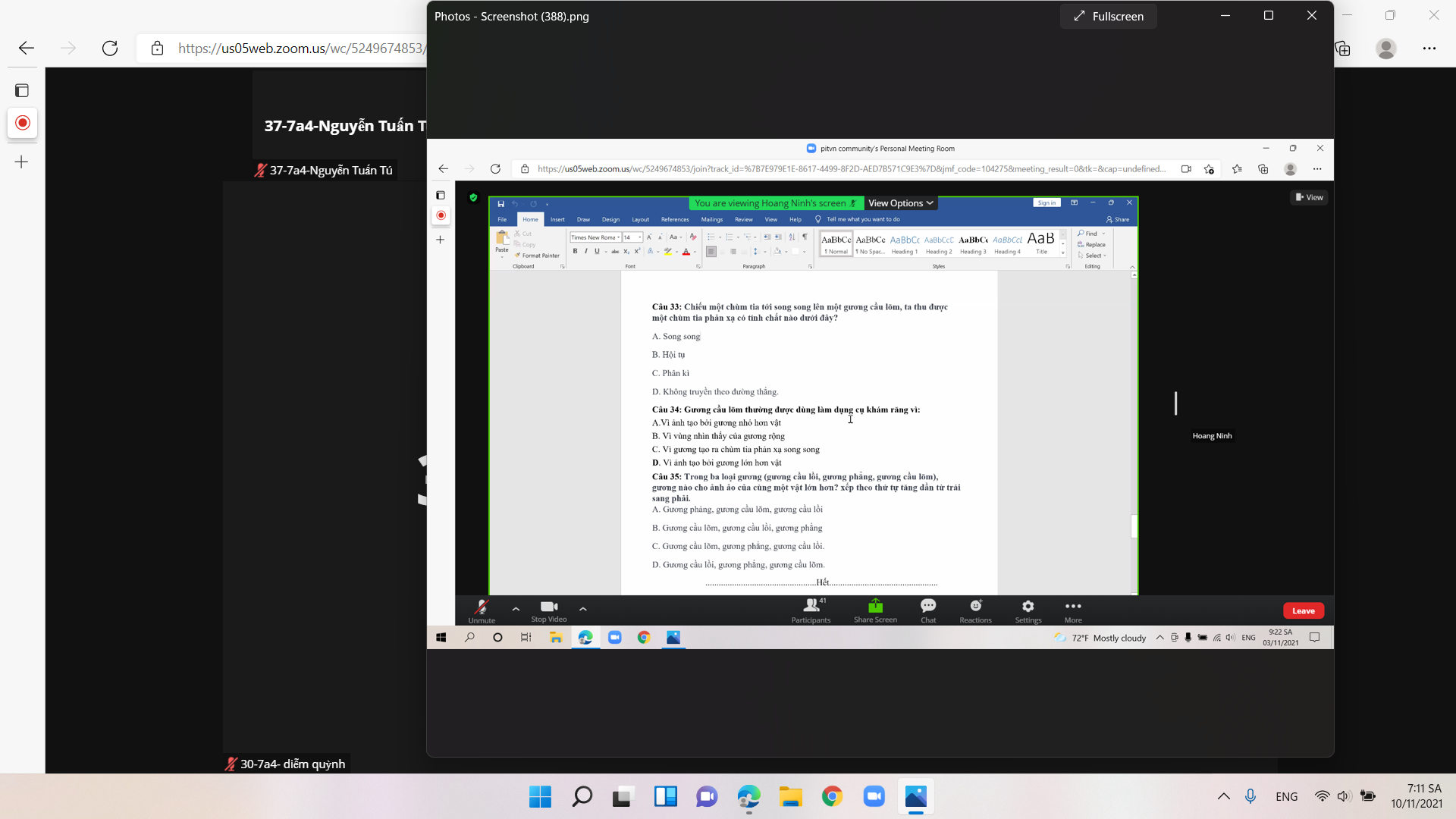
Giúp tui câu 33 34
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
S
2
H9
HT.Phong (9A5)
CTVHS
30 tháng 6 2023
\(M=\left[\left(\dfrac{2}{193}-\dfrac{3}{386}\right)\cdot\dfrac{193}{17}+\dfrac{33}{34}\right]:\left[\left(\dfrac{7}{2001}+\dfrac{11}{4002}\right)\cdot\dfrac{2001}{25}+\dfrac{9}{2}\right]\)
\(M=\left[\left(\dfrac{4}{386}-\dfrac{3}{386}\right)\cdot\dfrac{193}{17}+\dfrac{33}{34}\right]:\left[\left(\dfrac{14}{4002}+\dfrac{11}{4002}\right)\cdot\dfrac{2001}{25}+\dfrac{9}{2}\right]\)
\(M=\left(\dfrac{1}{386}\cdot\dfrac{193}{17}+\dfrac{33}{34}\right):\left(\dfrac{25}{4002}\cdot\dfrac{2001}{25}+\dfrac{9}{2}\right)\)
\(M=\left(\dfrac{1}{34}+\dfrac{33}{34}\right):\left(\dfrac{1}{2}+\dfrac{9}{2}\right)\)
\(M=1:5\)
\(M=\dfrac{1}{5}\)
30 tháng 6 2023
\(=\left[\dfrac{4-3}{386}\cdot\dfrac{193}{17}+\dfrac{33}{34}\right]:\left[\dfrac{25}{4002}\cdot\dfrac{2001}{25}+\dfrac{9}{2}\right]\)
\(=\left(\dfrac{1}{34}+\dfrac{33}{34}\right):\left[\dfrac{1}{2}+\dfrac{9}{2}\right]\)
=1/5
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 3 2022
33. B là khẳng định sai
Câu này xác định rất đơn giản, AB và AC cùng thuộc mp (ABC), trong khi MN không song song và cũng ko thuộc (ABC) nên 3 vecto này ko thể đồng phẳng
34.
\(\overrightarrow{MN}=\overrightarrow{MD'}+\overrightarrow{D'C'}+\overrightarrow{C'N}=\dfrac{1}{3}\overrightarrow{AD'}+\overrightarrow{D'C'}+\dfrac{1}{3}\overrightarrow{C'D}\)
\(=\dfrac{1}{3}\overrightarrow{AD}+\dfrac{1}{3}\overrightarrow{AA'}+\overrightarrow{D'C'}+\dfrac{1}{3}\overrightarrow{C'C}+\dfrac{1}{3}\overrightarrow{C'D'}\)
\(=\dfrac{1}{3}\overrightarrow{AD}+\dfrac{2}{3}\overrightarrow{D'C'}=-\dfrac{1}{3}\overrightarrow{AD}+\dfrac{2}{3}\left(B'C'+\overrightarrow{A'B'}\right)\)
\(=-\dfrac{1}{3}\overrightarrow{AD}+\dfrac{2}{3}\overrightarrow{A'C'}\)
A là đáp án đúng
22 tháng 4 2023
Câu 33:
\(n_{C_6H_2Br_3\left(OH\right)}=\dfrac{4,965}{331}=0,015\left(mol\right)\)
PT: \(C_6H_5OH+3Br_2\rightarrow C_6H_2Br_3\left(OH\right)+3HBr\)
Theo PT: \(n_{Br_2}=3n_{C_6H_2Br_3\left(OH\right)}=0,045\left(mol\right)\)
\(\Rightarrow m_{Br_2}=0,045.160=7,2\left(g\right)\)
Đáp án: D
22 tháng 4 2023
Câu 34:
Ta có: 94nC6H5OH + 32nCH3OH = 15,8 (1)
PT: \(C_6H_5OH+Na\rightarrow C_6H_5ONa+\dfrac{1}{2}H_2\)
\(CH_3OH+Na\rightarrow CH_3ONa+\dfrac{1}{2}H_2\)
Theo PT: \(n_{H_2}=\dfrac{1}{2}n_{C_6H_5ONa}+\dfrac{1}{2}n_{CH_3OH}=\dfrac{3,36}{22,4}=0,15\left(mol\right)\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}n_{C_6H_5OH}=0,1\left(mol\right)\\n_{CH_3OH}=0,2\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\%n_{CH_3OH}=\dfrac{0,2}{0,1+0,2}.100\%\approx66,67\%\)
Đáp án: C
NH
2
VN
Võ Ngọc Phương
VIP
1 tháng 8 2023
\(D=1+3+3^2+3^3+3^4+...+3^{2022}\)
\(3D=3.\left(1+3+3^2+3^3+3^4+...+3^{2022}\right)\)
\(3D=3+3^2+3^3+3^4+3^5+...+3^{2023}\)
\(3D-D=\left(3+3^2+3^3+3^4+3^5+...+3^{2023}\right)-\left(1+3+3^2+3^3+3^4+...+3^{2022}\right)\)
\(2D=\left(3^{2023}-1\right)\)
\(D=\left(3^{2023}-1\right):2\)
1 tháng 8 2023
3D=3+3^2+...+3^2023
=>2D=3^2023-1
=>\(D=\dfrac{3^{2023}-1}{2}\)
OS
1