Chỉ cần phần b chứng minh đến hình bình hành là đc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 11 2021
b: Xét tứ giác ADME có
AD//ME
AE//DM
Do đó: ADME là hình bình hành
CH
Cô Hoàng Huyền
Admin
VIP
23 tháng 7 2018
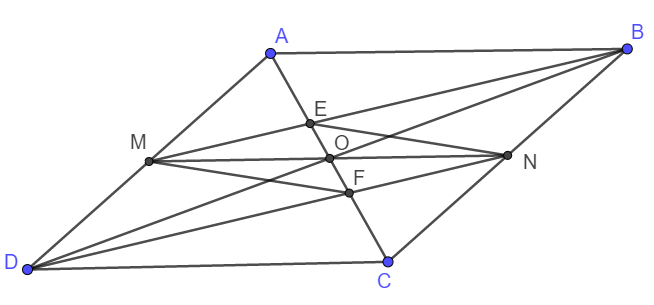
a) Do ABCD là hình bình hành nên AD song song và bằng BC.
Lại có M, N là trung điểm AD, BC nên DM song song và bằng BN. Suy ra DMBN là hình bình hành, hay MB//DN.
Xét tam giác ADF, có:
M là trung điểm AC
ME//DF
\(\Rightarrow\) ME là đường trung bình tam giác ADF.
Vậy AE = EF.
Hoàn toàn tương tự : EF = FC.
Vậy nên AE = EF = FC.
b) DMBN là hình bình hành nên hai đường chéo DB và MN cắt nhau tại trung điểm mỗi đường.
Vậy thì O là trung điểm MN.
Lại có: AO = OC; AE = FC nên AO - AE = OC - FC hay EO = OF.
Xét tứ giác MENF có O là trung điểm hai đường chéo EF và MN nên MENF là hình bình hành.
c)
+) Để hình bình hành MENF là hình chữ nhật thì hai đường chéo MN và EF bằng nhau.
Lại có MN = AB, EF = \(\frac{AC}{3}\). Vậy hình bình hành ABCD phải có đường chéo AC = 2AB thì MENF là hình chữ nhật.
+) Để hình bình hành MENF là hình thoi thì hai đường chéo MN và EF phải vuông góc.
Vậy thì \(EF\perp MN\Rightarrow AC\perp AB\)
Vậy hình bình hành ABCD phải có đường chéo AC vuông góc với cạnh AB thì MENF là hình thoi.
+) Để hình bình hành MENF là hình vuông thì nó vừa là hình chữ nhật, vừa là hình thoi.
Vậy thì hình bình hành ABCD có đường chéo AC vuông góc với AB và AC = 2AB.
TK
25 tháng 9 2017
Gọi O la giao điểm hai đường chéo hình bình hành
Từ O kẻ OO' vông góc với d tại O'
Ta có O' là trg điểm của A'O (do cùng vuông góc và song song với D' trên duog thẳng d )
suy ra OO'là dg trg bình cua tam giac AAC
suy ra AA' = 2 OO'(1)
Ta có DD' song song BB' ( do cùng vuông óc với d)
suy ra DD' ,BB' là hình thang
Ta có
OO' song song DD' song song BB' (cùng vuông góc d)(a)
Và O là trug điểm DB(b(
Từ (a) và(b) suy ra O là trung điểm D'B'
suy ra OO là dg2 trung bình của bình thang DD' BB'
suy ra OO' là dg trug bình của hình thang DD' BB'
suy ra D'B' =2OO' (2)
Từ (1) và (2) suy ra AA' =BB' +DD'
nhớ cho mình nha
CM
3 tháng 9 2017
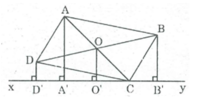
Gọi O là giao điểm của hai đường chéo AC và BD.
Kẻ OO' ⊥ xy
Ta có: BB' ⊥ xy (gt)
DD' ⊥ xy (gt)
Suy ra: BB // OO' // DD'
Tứ giác BB'D'D là hình thang .
OB = OD (t/chất hình bình hành)
Nên O'B' = O'D'
Do đó OO' là đường trung bình của hình thang BB'D'D
⇒ OO' = (BB' + DD') / 2 (tính chất đường trung hình hình thang) (1)
AA' ⊥ xy (gt)
OO' ⊥ xy (theo cách vẽ)
Suy ra: AA' // OO'
Trong ∆ ACA' tacó: OA = OC (tính chất hình bình hành)
OO' // AA' nên OO' là đường trung bình của ∆ ACA'
⇒ OO' = 1/2 AA' (tính chất đường trung bình của tam giác)
⇒ AA' = 2OO' (2)
Tử (1) và (2) suy ra: AA' = BB' + DD'
4 tháng 9 2016
![[IMG]](http://d.f11.photo.zdn.vn/upload/original/2012/07/25/20/15/1343222151615470685_574_574.jpg)
+Gọi giao điểm của AC và BD là O\Rightarrow O là trung điểm của AC và BD
+Kẻ OO' vuông góc với xy
+Xét hình thang DD'BB' (DD'//BB')
Có O là trung điểm DB mà OO'//BB'
=> OO' là đường trung bình
=> 2OO'=DD'+BB'(*)
Xét AA'C,có :OO'//AA',O là trung điểm của AC
=> OO' là đường trung bình
=> 2OO'=AA'(*) (*)
Từ (*) và (**) => đpcm
a: góc EAM=góc EMA
=>ΔEAM cân tại E
=>Em=EA
=>OE là trung trực của MA
=>OE vuông gócAM tại I
góc OIM+góc OPM=180 độ
=>OPMI nội tiếp
EM vuông góc OM
=>EM là tiếp tuyến của đường tròn đường kính OM
b: góc HMA=góc MAO
=>H nằm trên OE là trung trực của AM
=>HA=HM
=>ΔHAM cân tại H
=>góc HMA=góc HAM
=>ΔHAM=ΔOMA
=>HA=HM=OA=OM
=>AHMO là hình thoi