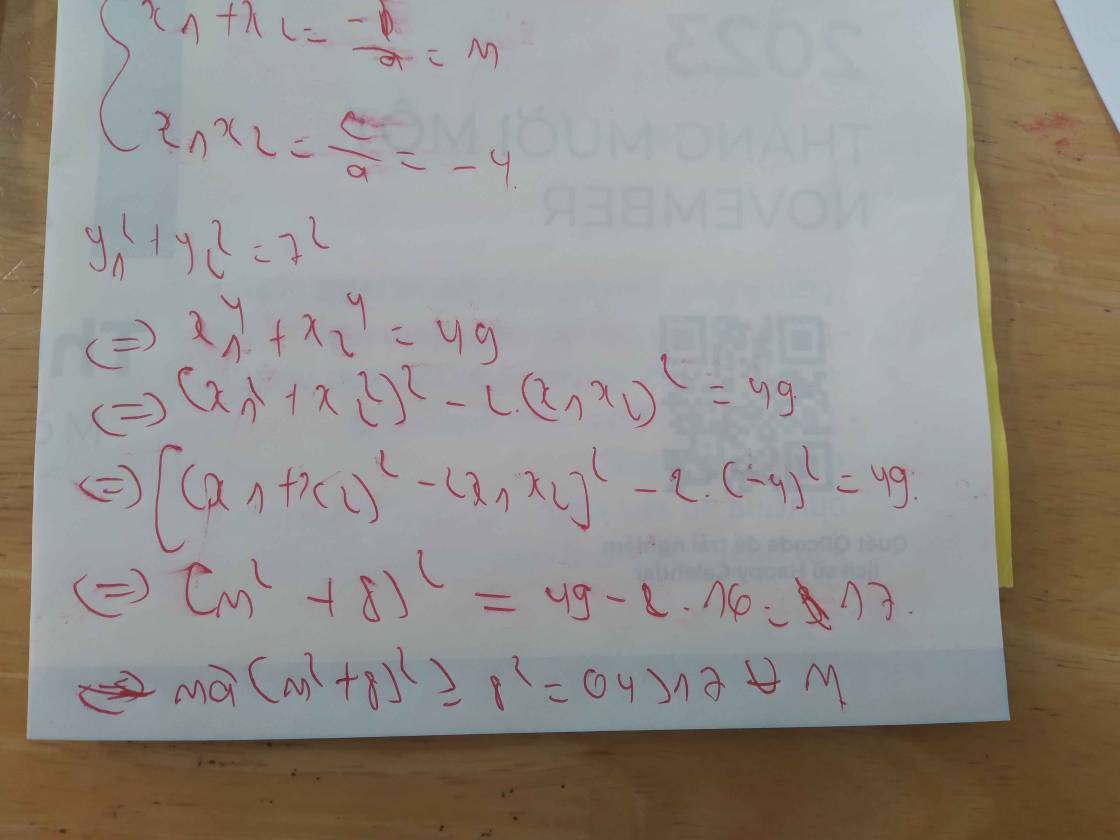Cho parabol (p):y=x^2 và đường thẳng (d):y=-4x+2m-1(Với m là tham số) .Gọi x1 và x2 là hoành độ giao điểm của (p) và (d ) . tìm m để x1^2 -x2 =2m .Mọi người giải hộ mình vs mai mình cần rồi!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 4 2021
Phương trình hoành độ giao điểm (d) và (P):
\(x^2=\left(m+2\right)x-2m\Leftrightarrow x^2-\left(m+2\right)x+2m=0\) (1)
(d) cắt (P) tại 2 điểm pb khi và chỉ khi (1) có 2 nghiệm pb
\(\Leftrightarrow\Delta=\left(m+2\right)^2-8m>0\)
\(\Leftrightarrow\left(m-2\right)^2>0\Leftrightarrow m\ne2\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m+2\\x_1x_2=2m\end{matrix}\right.\)
\(x_1^2+\left(m+2\right)x_2=12\)
\(\Leftrightarrow x_1\left(x_1+x_2\right)-x_1x_2+\left(m+2\right)x_2=12\)
\(\Leftrightarrow\left(m+2\right)x_1-2m+\left(m+2\right)x_2=12\)
\(\Leftrightarrow\left(m+2\right)\left(x_1+x_2\right)-2m-12=0\)
\(\Leftrightarrow\left(m+2\right)^2-2m-12=0\)
\(\Leftrightarrow m^2+2m-8=0\Rightarrow\left[{}\begin{matrix}m=-4\\m=2\left(loại\right)\end{matrix}\right.\)
DD
Đoàn Đức Hà
Giáo viên
23 tháng 4 2022
Phương trình hoành độ giao điểm của \(\left(d\right)\) và \(\left(P\right)\) là:
\(x^2=2mx+3\Leftrightarrow x^2-2mx-3=0\) (1)
Phương trình (1) có hệ số \(a.c=1.\left(-3\right)=-3< 0\) nên (1) luôn có hai nghiệm phân biệt \(x_1,x_2\).
Theo hệ thức Viete ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-3\end{matrix}\right.\)
Ta có: \(\left|x_1\right|+3\left|x_2\right|=6\)
Ta có hệ:
\(\left\{{}\begin{matrix}x_1x_2=-3\\\left|x_1\right|+3\left|x_2\right|=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-\dfrac{3}{x_2}\\\left|\dfrac{3}{x_2}\right|+3\left|x_2\right|=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-\dfrac{3}{x_2}\\x_2^2-2\left|x_2\right|+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x_2=-1,x_1=3\\x_2=1,x_1=-3\end{matrix}\right.\)
Với \(x_1=3,x_2=-1\Rightarrow x_1+x_2=2\Rightarrow m=1\).
Với \(x_1=-3,x_2=1\Rightarrow x_1+x_2=-2\Rightarrow m=-1\)
23 tháng 4 2022
Phương trình hoành độ giao điểm của và là:
(1)
Phương trình (1) có hệ số nên (1) luôn có hai nghiệm phân biệt .
Theo hệ thức Viete ta có:
Ta có:
Ta có hệ:
Với .
Với
AH
Akai Haruma
Giáo viên
22 tháng 5 2021
Lời giải:
PT hoành độ giao điểm:
$x^2-2mx-(2m+1)=0(*)$
Để (P) và (d) cắt nhau tại 2 điểm pb có hoành độ $x_1,x_2$ thì PT $(*)$ phải có 2 nghiệm pb $x_1,x_2$
$\Leftrightarrow \Delta'=m^2+2m+1>0\Leftrightarrow (m+1)^2>0$
$\Leftrightarrow m\neq -1$
Áp dụng định lý Viet: $x_1+x_2=2m; x_1x_2=-(2m+1)$
Khi đó:
$\sqrt{x_1+x_2}+\sqrt{3+x_1x_2}=2m+1$
$\Leftrightarrow \sqrt{2m}+\sqrt{3-2m-1}=2m+1$
\(\Leftrightarrow \left\{\begin{matrix}
0\leq m< 1\\
\sqrt{2m}+\sqrt{2(1-m)}=2m+1\end{matrix}\right.\)
Bình phương 2 vế dễ dàng giải ra $m=\frac{1}{2}$ (thỏa)