Một đội công nhân A và B làm chung một công việc và dự định hoàn thành trong 12 ngày. Khi làm chung được 8 ngày thì đội A được điều động đi làm việc khác, đội B tiếp tục làm phần việc còn lại. Kể từ khi làm một mình, do cải tiến cách làm nên năng suất của đội B tăng gấp đôi, do đó đội B đã hoàn thành phần việc còn lại trong 8 ngày tiếp theo. Hỏi với năng suất ban đầu thì mỗi đội làm một mình sẽ hoàn thành công việc đó trong bao lâu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi thời gian đội I làm một mình để hoàn thành công việc là x ( đơn vị ngày, x > 12 )
Gọi thời gian đội II làm một mình để hoàn thành công việc là y ( đơn vị ngày, y > 12 )
Mỗi ngày đội I làm được \(\dfrac{1}{x}\) ( công việc )
Mỗi ngày đội II làm được \(\dfrac{1}{y}\) ( công việc )
8 ngày làm được \(\dfrac{2}{3}\) ( công việc )
Năng suất mới của đội II là \(\dfrac{2}{y}\) ( công việc )
theo đề bài ta có hệ pt :
1/x + 1/y = 1/12 và 2/3 + 2/y . 7/2 = 1
Giải hệ pt ta đc x = 28 , y = 21 (tm )
kết luận

Gọi x,y là số ngày đội 1 ; đội 2 làm xong công việc \((x;y>12)\)
Trong 1 ngày đội 1 làm được \(\frac{1}{x}\)công việc
Trong 1 ngày đội 2 làm được \(\frac{1}{y}\)công việc
Trong 1 ngày cả hai đội làm được \(\frac{1}{12}\)công việc
Theo bài ra,ta có : \(\frac{1}{x}+\frac{1}{y}=\frac{1}{12}(1)\)
Khi cả hai đội làm chung 8 ngày,cả hai đội làm được : \(\frac{8}{12}=\frac{2}{3}\)công việc
Số công việc còn lại để đội 2 làm nốt là : \(1-\frac{2}{3}=\frac{1}{3}\)công việc
Đội 2 làm năng suất gấp đôi : \(2\cdot\frac{1}{y}=\frac{2}{y}\)
Theo bài ra,ta có : \(7\cdot\frac{2}{y}=\frac{1}{3}\)
Từ 1 và 2 bạn tự suy ra nhé
Chúc bạn học tốt

Gọi thời gian đội I và đội II làm một mình xong công việc lần lượt là x; y (ngày)
Điều kiện : x, y > 12, x,y ∈ N.
Một ngày đội I làm được : 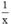 (công việc).
(công việc).
Một ngày đội II làm được :  (công việc).
(công việc).
+ Hai đội cùng làm sẽ xong trong 12 ngày nên ta có phương trình: 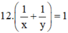
+ Hai đội cùng làm trong 8 ngày được: 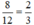 công việc.
công việc.
⇒ còn lại đội II phải hoàn thành một mình 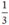 công việc.
công việc.
Vì đội II tăng năng suất gấp đôi nên một ngày đội II làm được 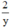 công việc.
công việc.
Đội II hoàn thành 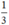 công việc còn lại trong 3,5 ngày nên ta có phương trình:
công việc còn lại trong 3,5 ngày nên ta có phương trình: 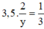
Ta có hệ phương trình:
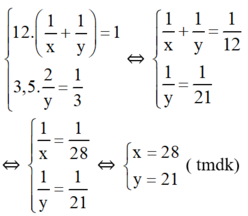
Vậy nếu làm một mình, đội I làm xong công việc trong 28 ngày, đội II làm xong công việc trong 21 ngày.

Gọi thời gian đội I và đội II làm một mình xong công việc lần lượt là x; y (ngày)
Điều kiện : x, y > 12, x,y ∈ N.
Một ngày đội I làm được : 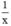 (công việc).
(công việc).
Một ngày đội II làm được :  (công việc).
(công việc).
+ Hai đội cùng làm sẽ xong trong 12 ngày nên ta có phương trình: 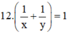
+ Hai đội cùng làm trong 8 ngày được: 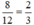 công việc.
công việc.
⇒ còn lại đội II phải hoàn thành một mình 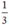 công việc.
công việc.
Vì đội II tăng năng suất gấp đôi nên một ngày đội II làm được 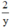 công việc.
công việc.
Đội II hoàn thành 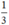 công việc còn lại trong 3,5 ngày nên ta có phương trình:
công việc còn lại trong 3,5 ngày nên ta có phương trình: 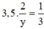
Ta có hệ phương trình:
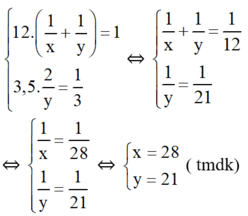
Vậy nếu làm một mình, đội I làm xong công việc trong 28 ngày, đội II làm xong công việc trong 21 ngày.

Gọi (ngày) là thời gian đội I làm một mình xong công việc với năng suất ban đầu ,
(ngày) là thời gian đội II làm một mình xong công việc với năng suất ban đầu
Trong 1 ngày đội I làm được (công việc),
đội II làm được (công việc)
Hai đội xây dựng làm chung theo dự định trong 12 ngày xong nên ta có:
(1)
Cả hai đội làm chung 8 ngày thì được (công việc)
Số công việc còn lại của đội II làm là: (công việc)
Năng suất của đội II tăng gấp 2 lần nên 1 ngày làm được công việc
Khi năng suất tăng họ làm 3,5 ngày thì hoàn thành phần công việc còn lại nên ta có:
(2)
Thay vào (1) suy ra
Vậy nếu làm theo dự định thời gian đội I làm một mình xong công việc là ngày, thời gian đội II làm một mình xong công việc là ngày.
Gọi x,y theo thứ tư là thời gian mà mỗi đội làm một mình thì hoàn thành công việc.
Với năng suất ban đầu: x,y > 0 và tính theo đơn vị ngày.
Trong 1 ngày đội I làm được 1/x công việc. 1 ngày đội II làm được 1/y công việc. 1 ngày cả 2 đội làm được 1/12 công việc.
Ta có phương trình: 1/x + 1/y = 1/12 (công việc)( 1)
Trong 8 ngày cả hai đội làm được 8. 1/12 = 2/3 (công việc).
Sau khi một đội nghỉ, năng suất của đội II là 2/y. Họ phải làm trong 3,5 ngày thì xong công việc nên ta có phương trình 1/3 : 2/y = 7/2
(2)
Ta có hệ:Giải hệ1,2 này, ta được x = 28 (ngày); y = 21(ngày) Chú ý: Ta có thể đặt hệ

Gọi A là số công việc đội 1 và đội 2 làm được trong 1 ngày.
Gọi B là số công việc đội 3 làm được trong 1 ngày.
Cả 3 đội trong 1 ngày làm được A + B công việc
Theo bài ra ta có hệ phương trình
4 * (A + B) + 12 * A = 1 hay 4A +4B + 12A = 1 hay 16A +4B = 1 (1)
6 * (A + B) + 9 * A = 1 hay 6A + 6B + 9A =1 hay 15A + 6B = 1 (2)
Nhân (1) với 3, nhân (2) với 2 ta có hệ
48A + 12B = 3 (3)
30A + 12B = 2 (4)
Trừ (3) cho (4) ta có
18A = 1, suy ra A = 1/18
Thời gian chỉ đội 1 và đội 2 cùng làm hoàn thành công việc là
1 : 1/18 = 18 ngày
Vậy chỉ đội 1 và đội 2 cùng làm thì sau 18 ngày sẽ hoàn thành công việc.

so cong viec la 1, 1 ngay thi doi 1 lam dc 1/x cong viec, doi 2 lam dc 1/y cong viec
nen => moi ngay 2 doi lam dc 1/x cong 1/y cong viec, ca 2 doi phai mat 12 ngay moi hoan thanh xong cv nen moi ngay ho lam dc 1/12 cv => pt1
trong vong 8 ngay thi 2 doi hoan thanh dc 8*(1/x cong 1/y) =8/x cong 8/y
so cong viec con lai doi 2 phai lam, nhung vi nang suat cua ho tang gap 2 => so công viec moi ngay cua ho lam dc la 2/y
ho phai lam trong 3,5 ngay moi xong nen trong 3,5 ngay do ho lam dc 3,5*2/y
tong so cong viêc ca 2 doi lam trong 8 ngay cong voi so cong viêc con lai doi 2 hoan thanh la 1 => pt2
1 ngày đội I làm đc 1/x (phần công việc)
Trog 8 ngày đội I làm đc 8/x (phần công việc)
1 ngày đội II làm đc 1/y (phần công việc)
Trog 8 ngày đội II làm đc 8/y (phần công việc)
Vì năng suất của đội II tăng gấp đôi và họ đã làm xong công vc trong 3.5 ngày nên trog 3,5 ngày làm đc: 3,5.2/ y
Mà tổng số cv của cả 2 đội là 1 nên ta có PT:
8/x+ 8/ y + 3,5.2/ y = 1

Gọi thời gian đội I và đội II làm một mình xong công việc lần lượt là x; y ( ngày )
Điều kiện : \(x,y>12 ; x,y\in N\)
Một ngày đội I làm được : \(\frac{1}{x}\)công việc
Một ngày đội II làm được : \(\frac{1}{y}\)công việc
+ Hai đội cùng làm sẽ xong trong 12 ngày nên ta có phương trình : \(12.\left(\frac{1}{x}+\frac{1}{y}\right)=1\)
+ Hai đội cùng làm trong 8 ngày được : \(\frac{8}{12}=\frac{2}{3}\)công việc
=> Còn lại đội II phải hoàn thành một mình \(\frac{1}{3}\)công việc
Vì đội II tăng năng suất gấp đôi nên một ngày đội II làm được \(\frac{2}{y}\)công việc
Đội II hoàn thành \(\frac{1}{3}\)công việc còn lại trong 3,5 ngày nên ta có PT : \(3,5.\frac{2}{y}=\frac{1}{3}\)
Ta có HPT : \(\hept{\begin{cases}12.\left(\frac{1}{x}+\frac{1}{y}\right)=1\\3,5.\frac{2}{y}=\frac{1}{3}\end{cases}\Leftrightarrow\hept{\begin{cases}\frac{1}{x}+\frac{1}{y}=\frac{1}{12}\\\frac{1}{y}=\frac{1}{21}\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}\frac{1}{x}=\frac{1}{28}\\\frac{1}{y}=\frac{1}{21}\end{cases}\Leftrightarrow}\hept{\begin{cases}x=28\\y=21\end{cases}\left(tmđk\right)}\)
Vậy nếu làm một mình, đội I làm xong công việc trong 28 ngày, đội II làm xong công việc trong 21 ngày