Giải bài hộ mk nha.huhu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
2
CU
6 tháng 3 2016
Cường có số thời gian rảnh rỗi là: \(1-\frac{1}{3}-\frac{1}{6}-\frac{1}{12}-\frac{1}{8}-\frac{1}{24}=\frac{1}{4}\)
H9
HT.Phong (9A5)
CTVHS
30 tháng 6 2023
1) \(\sqrt{11-6\sqrt{2}}-\sqrt{6-4\sqrt{2}}\)
\(=\sqrt{9-6\sqrt{2}+2}-\sqrt{4-4\sqrt{2}+2}\)
\(=\sqrt{3^2-2\cdot3\cdot\sqrt{2}+\left(\sqrt{2}\right)^2}-\sqrt{2^2-2\cdot2\cdot\sqrt{2}\cdot\left(\sqrt{2}\right)^2}\)
\(=\sqrt{\left(3-\sqrt{2}\right)^2}-\sqrt{\left(2-\sqrt{2}\right)^2}\)
\(=\left|3-\sqrt{2}\right|-\left|2-\sqrt{2}\right|\)
\(=3-\sqrt{2}-2+\sqrt{2}=1\)
2) \(\sqrt{\left(1-\sqrt{2}\right)^2}-\sqrt{\left(2-\sqrt{2}\right)^2}\)
\(=\left|1-\sqrt{2}\right|-\left|2-\sqrt{2}\right|\)
\(=\sqrt{2}-1+2-\sqrt{2}\)
\(=1\)
3) \(\sqrt{\left(2\sqrt{2}-1\right)^2}-\sqrt{17+12\sqrt{2}}\)
\(=\sqrt{\left(2\sqrt{2}-1\right)^2}-\sqrt{9+12\sqrt{2}+8}\)
\(=\sqrt{\left(2\sqrt{2}-1\right)^2}-\sqrt{3^2+2\cdot3\cdot2\sqrt{2}+\left(2\sqrt{2}\right)^2}\)
\(=\sqrt{\left(2\sqrt{2}-1\right)^2}-\sqrt{\left(3+2\sqrt{2}\right)^2}\)
\(=\left|2\sqrt{2}-1\right|-\left|3+2\sqrt{2}\right|\)
\(=2\sqrt{2}-1-3-2\sqrt{2}=-4\)
4) \(\sqrt{\left(2-\sqrt{5}\right)^2}+\sqrt{14-6\sqrt{5}}\)
\(=\sqrt{\left(2-\sqrt{5}\right)^2}+\sqrt{9-6\sqrt{5}+5}\)
\(=\sqrt{\left(2-\sqrt{5}\right)^2}+\sqrt{3^2-2\cdot3\cdot\sqrt{5}+\left(\sqrt{5}\right)^2}\)
\(=\sqrt{\left(2-\sqrt{5}\right)^2}+\sqrt{\left(3-\sqrt{5}\right)^2}\)
\(=\left|2-\sqrt{5}\right|+\left|3-\sqrt{5}\right|\)
\(=\sqrt{5}-2+3-\sqrt{5}=1\)
5) \(\sqrt{\left(4-3\sqrt{2}\right)^2}-\sqrt{19+6\sqrt{2}}\)
\(=\sqrt{\left(4-3\sqrt{2}\right)^2}-\sqrt{18+6\sqrt{2}+1}\)
\(=\sqrt{\left(4-3\sqrt{2}\right)^2}-\sqrt{\left(3\sqrt{2}\right)^2+2\cdot3\sqrt{2}\cdot1+1^2}\)
\(=\sqrt{\left(4-3\sqrt{2}\right)^2}-\sqrt{\left(3\sqrt{2}+1\right)^2}\)
\(=\left|4-3\sqrt{2}\right|-\left|3\sqrt{2}+1\right|\)
\(=3\sqrt{2}-4-3\sqrt{2}-1=-5\)
6) \(\sqrt{3-2\sqrt{2}}+\sqrt{\left(2-\sqrt{2}\right)^2}\)
\(=\sqrt{2-2\sqrt{2}+1}+\sqrt{\left(2-\sqrt{2}\right)^2}\)
\(=\sqrt{\left(\sqrt{2}\right)^2-2\cdot\sqrt{2}\cdot1+1^2}+\sqrt{\left(2-\sqrt{2}\right)^2}\)
\(=\sqrt{\left(\sqrt{2}-1\right)^2}+\sqrt{\left(2-\sqrt{2}\right)^2}\)
\(=\sqrt{2}-1+2-\sqrt{2}=1\)
29 tháng 6 2023
1: =3-căn 2-2+căn 2=1
2: \(=\sqrt{2}-1+2-\sqrt{2}=1\)
3: \(=2\sqrt{2}-1-3-2\sqrt{2}=-4\)
4: \(=\sqrt{5}-2+3-\sqrt{5}=1\)
5: \(=3\sqrt{2}-4-3\sqrt{2}-1=-5\)
6: \(=\sqrt{2}-1+2-\sqrt{2}=1\)
NK
1
VC
Vũ Cao Minh⁀ᶦᵈᵒᶫ ( ✎﹏IDΣΛ亗 )
CTV
VIP
20 tháng 7 2021
a) Góc xAK kề bù với góc 115 độ nên góc xAK = 650
Vì Ky song song với Ax nên góc AKy = xAk = 650 ( so le trong )
b) Vì Ky song song với Mz nên zMK + yKM = 1800 ( trong cùng phía ) => góc yKM = 350
=> góc AKM = AKy + yKM = 550 + 350 = 900 hay AK vuông góc với MK
1 tháng 3 2022
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó; ΔABM=ΔACM
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
Suy ra: AE=AF và ME=MF
hay ΔMEF cân tại M
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
30 tháng 9 2021
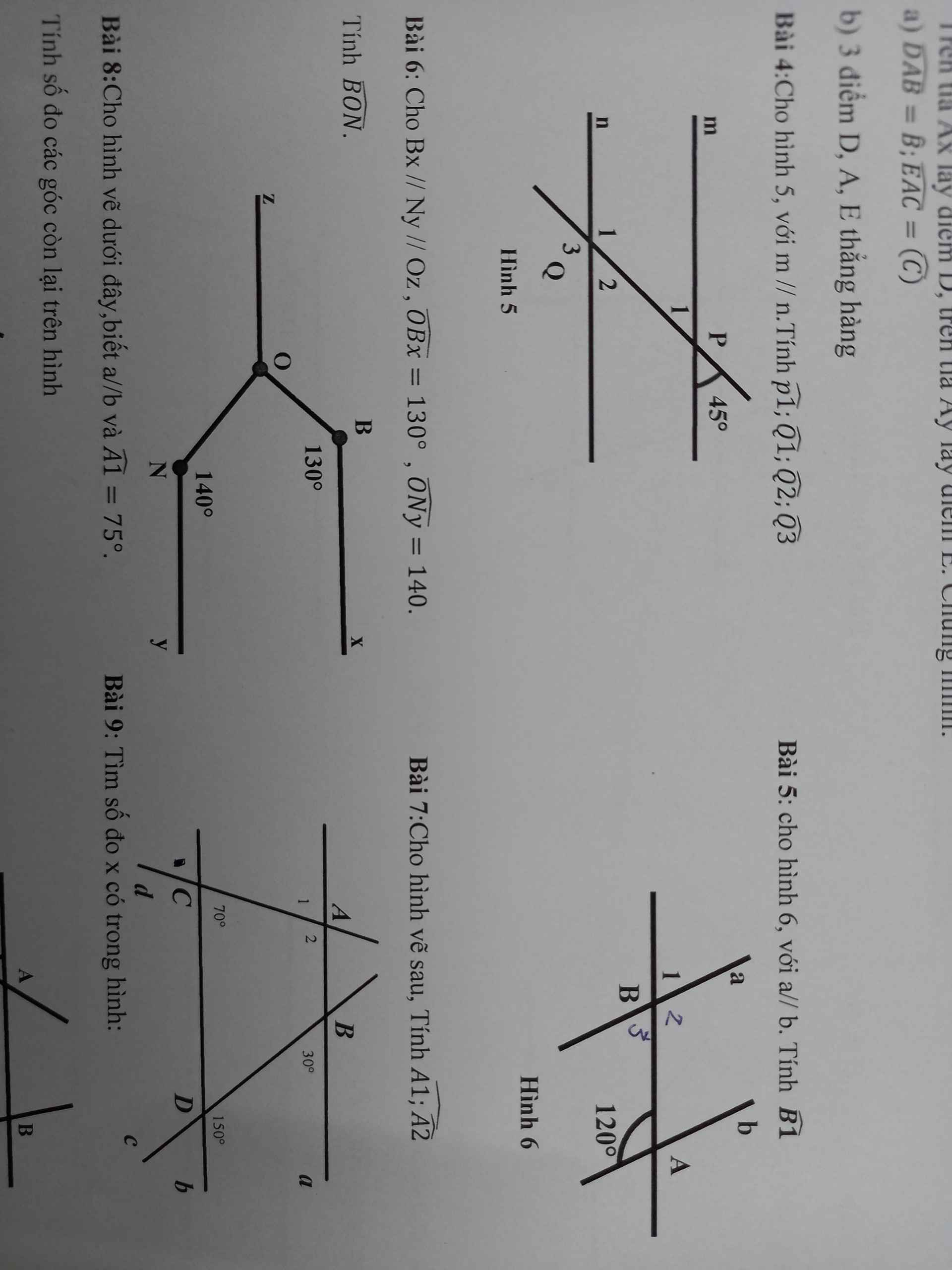
bài 5
góc BAb=1800-1200=600
mà B1=góc BAb=600(so le trong)
bài 7
có góc BDC=1800- góc BDb=1800-1500=300
=>góc BDC= góc aBD
=>a//b
=>A1=góc ACD=700
=>A2=1800-ACD=1800-700=1100
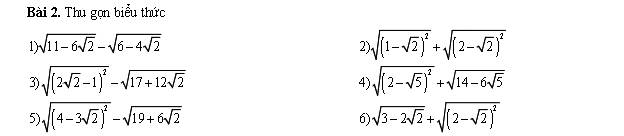
Bài nào?