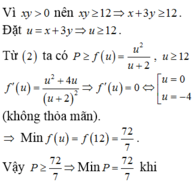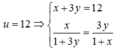tìm giá trị nhỏ nhất của biểu thức x - 2canxy + 3y - 2canx + 2009.5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 12 2021
Bài 1:
\(A=x^2+6x+9+x^2-10x+25\)
\(=2x^2+4x+34\)
\(=2\left(x^2+2x+17\right)\)
\(=2\left(x+1\right)^2+32>=32\forall x\)
Dấu '=' xảy ra khi x=-1
LT
0
1
1
5 tháng 2 2022
\(P=\dfrac{3}{x}+\dfrac{1}{3y}=\dfrac{3}{x}+\dfrac{\dfrac{1}{3}}{y}\ge\dfrac{\left(\sqrt{3}+\dfrac{1}{\sqrt{3}}\right)^2}{x+y}=\dfrac{\dfrac{16}{3}}{\dfrac{4}{3}}=4\)
\(min_P=4\Leftrightarrow x=1;y=\dfrac{1}{3}\)
NN
0
VT
1
19 tháng 3 2020
A = (x - 5)2 + |3y - 6| - 3
Ta có
\(\hept{\begin{cases}\left(x-5\right)^2\ge0\\\left|3x-6\right|\ge0\end{cases}\forall x;y}\)
<=> (x - 5)2 + |3y - 6| \(\ge\) 0 \(\forall\) x ; y
<=> A = (x - 5)2 + |3y - 6| - 3 \(\ge\) 0 \(\forall\)x;y
Dấu "=" xảy ra <=> \(\hept{\begin{cases}\left(x-5\right)^2=0\\\left|3y-6\right|=0\end{cases}}\)
<=> \(\hept{\begin{cases}x-5=0\\3y-6=0\end{cases}}\)
<=> \(\hept{\begin{cases}x=5\\3x=6\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=5\\y=2\end{cases}}\)
Vậy Min A = - 3 <=> x =5 và y = 2
Học tốt
N
2
28 tháng 10 2018
A = \(x^2+9y^2+25+6xy-30y-10x-6xy+26\)
= \(x^2-10x+25+9y^2-30y+25+1\)
= \(\left(x-5\right)^2+\left(3y-5\right)^2+1\)
Có : \(\left(x-5\right)^2\ge0\forall x;\left(3y-5\right)^2\ge0\forall y\)
\(\Rightarrow A\ge1\)
Vậy GTNN của A là 1 \(\Leftrightarrow\hept{\begin{cases}x-5=0\\3y-5=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=5\\y=\frac{5}{3}\end{cases}}}\)
CM
26 tháng 2 2018
Theo bài ra ta có:
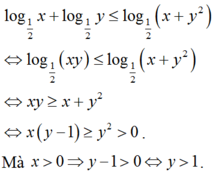
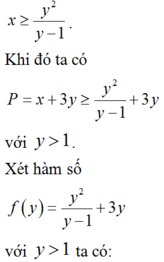
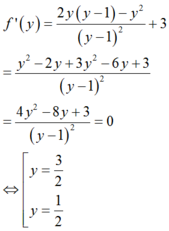
BBT:
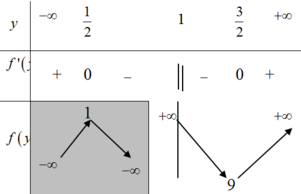
Từ BBT ta thấy
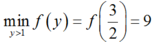
Vậy P ≥ 9 hay P m i n = 9 .
Chọn C.