Tìm số phức z thoả (2+i)^2 (1-i)z = 4 -3i +(3+i) z
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn D.
Ta có P = |2z + 1 = 2i| nên 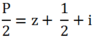
Ta cần tìm giá trị lớn nhất, giá trị nhỏ nhất của: 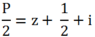
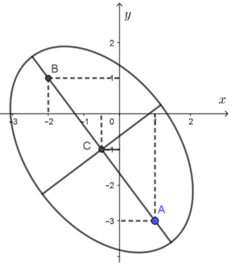
Ta có z1 = 1 - 3i; z2 = -2 + i và z0 = -1/2 - i
Ta thấy: ![]()
Tính 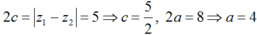
Suy ra 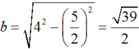
Vậy Max P = 2.4 = 8 và 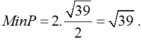

Đặt \(z=x+yi\Rightarrow\) quỹ tích z là các điểm M thuộc đường tròn \(\left(x-2\right)^2+\left(y+3\right)^2=5\) có tâm \(I\left(2;-3\right)\) bán kính \(R=\sqrt{5}\)
\(P=x^2+\left(y+1\right)^2-\left(x-2\right)^2-y^2=4x+2y-3\)
\(P=4\left(x-2\right)+2\left(y+3\right)-1\le\sqrt{\left(4^2+2^2\right)\left[\left(x-2\right)^2+\left(y+3\right)^2\right]}-1=11\)
\(\Rightarrow P_{max}=11\) khi \(\frac{x-2}{4}=\frac{y+3}{2}\Rightarrow x=2y+8\)
Thay vào \(\left(x-2\right)^2+\left(y+3\right)^2=5\) tìm được \(x;y\Rightarrow\) tìm được \(z\)

Chọn B.
Ta có: (2 - 3i).(1 + 2i) = 2 + 4i - 3i - 6i2 = 8 + i
Từ giả thiết : (1 + i)z + (2 - 3i)(1 + 2i) = 7 + 3i nên
(1 + i)z + (8 + i) = 7 + 3i hay (1 + i)z = -1 + 2i


Chọn D.
Giả sử z=a+bi với a,b ∈ ℝ
Thay vào biểu thức ta được:
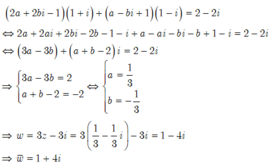


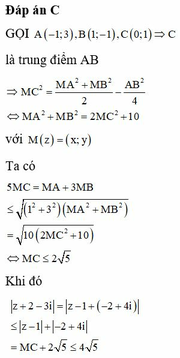
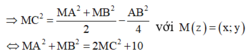
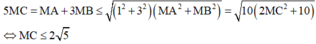
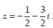
\(\Leftrightarrow\left(i^2+4i+4\right)\left(1-i\right)z=4-3i+\left(3+i\right)z\)
\(\Leftrightarrow\left(4i+3\right)\left(1-i\right)z-\left(3+i\right)z=4-3i\) (do \(i^2=-1\Rightarrow i^2+4=3\))
\(\Leftrightarrow\left(4i-4i^2+3-3i\right)z-\left(3+i\right)z=4-3i\)
\(\Leftrightarrow\left(7+i\right)z-\left(3+i\right)z=4-3i\)
\(\Leftrightarrow4z=4-3i\)
\(\Leftrightarrow z=1-\dfrac{3}{4}i\)