Gía trị lớn nhất của A= 4x-x2 là?
HELP HELP!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(A=-x\left(x-2\right)+2x-8=-x^2+2x+2x-8\\ =-x^2+4x-8\\ =-\left(x^2-4x+4\right)+4-8\\ =-\left(x-2\right)^2-4\)
Vì : \(\left(x-2\right)^2\ge0\forall x\)
\(=>-\left(x-2\right)^2\le0\)
\(=>A\le-4\)
Dấu = xảy ra khi : \(\left(x-2\right)^2=0=>x=2\)
Vậy GTLN bt A là : -4 tại x = 2

\(A=-x^2+4x+3\)
\(=-\left(x^2-4x+4-7\right)\)
\(=-\left(x^2-4x+4\right)+7\)
\(=-\left(x-2\right)^2+7\le7\)
Dấu = khi \(-\left(x-2\right)^2=0\Leftrightarrow x-2=0\Leftrightarrow x=2\)
Vậy \(Max_A=7\Leftrightarrow x=2\)


\(\dfrac{4x^2}{x^4+1}=\dfrac{-\left(4x^2+4x+1\right)+8x^2+4x+1}{x^4+1}\)
\(=-\dfrac{\left(2x+1\right)^2}{x^4+1}+\dfrac{8x^2+4x+1}{x^4+1}\)
mà \(-\dfrac{\left(2x+1\right)^2}{x^4+1}\le0\)
vậy M đạt GTLN khi x=-0,5
thay x=-0,5 vào biểu thức\(\dfrac{8x^2+4x+1}{x^4+1}\) , ta được KQ là \(\dfrac{16}{17}\)
vậy GTLN của M là \(\dfrac{16}{17}\) tại x=-0,5

Chọn B.
Phương pháp:
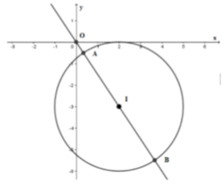
Biến đổi đẳng thức đã cho để đưa về dạng phương trình đường tròn (C) tâm I bán kính R.
Từ đó ta đưa bài toán về dạng bài tìm M x ; y ∈ C để O M - a lớn nhất hoặc nhỏ nhất.
Xét các trường hợp xảy ra để tìm a.
Cách giải:
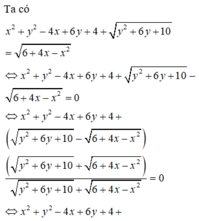
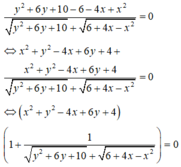


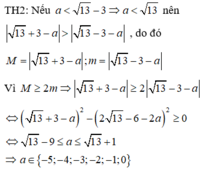


Chọn C
Hàm số y =
x
2
+
x
+
4
x
+
1
là hàm phân thức có tập xác định là ![]() nên nó liên tục trên [0;2], từ đó ta vận dụng quy tắc tìm giá trị lớn nhất và nhỏ nhất không cần xét dấu đạo hàm.
nên nó liên tục trên [0;2], từ đó ta vận dụng quy tắc tìm giá trị lớn nhất và nhỏ nhất không cần xét dấu đạo hàm.
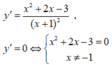
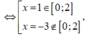
Ta có ![]()
=> A = 4, a = 3.
Vậy a + A = 7.