một vật ab = 2 cm được đặt vuông góc với trục chính của một thấu kính phân kì có tiêu cự 12 cm điểm A nằm trên trục chính cách thấu kính 12 cm a, vẽ ảnh b, tính độ cao
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
21 tháng 8 2017
a. Hình vẽ: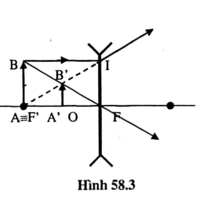
b. Ảnh ảo
c. Do A = F nên BO, AI là hai đường chéo của hình chữ nhật ABIO. B' là giao điểm của hai đường chéo BO, AI
=> A'B' là đường trung bình ΔABO
Nên OA' = 1/2.OA = 1/2.20= 10 (cm).
TH
15 tháng 3 2023
Để vẽ ảnh của vật AB, ta sử dụng công thức ảnh của thấu kính hội tụ:
1/f = 1/do + 1/di
Với f là tiêu cự của thấu kính, do là khoảng cách từ vật đến thấu kính, di là khoảng cách từ ảnh đến thấu kính.
a) Khi đặt điểm A cách thấu kính 20 cm (do = 20 cm)
Áp dụng công thức 1/f = 1/do + 1/di, ta tính được:
1/12 = 1/20 + 1/di
=> di = 30 cm
Do ảnh a'b' của vật AB nằm trên cùng trục với vật, nên a'b' cũng có chiều cao bằng 4 cm và nằm ở phía đối diện với vật (ảnh đối xứng với vật qua trung tâm của thấu kính).
Vậy, ảnh a'b' của vật AB sẽ có kích thước bằng với vật và nằm ở phía đối diện.
b) Khi đặt điểm A cách thấu kính 8 cm (do = 8 cm)
Áp dụng công thức 1/f = 1/do + 1/di, ta tính được:
1/12 = 1/8 + 1/di
=> di = 24 cm
Ở trường hợp này, do ảnh a'b' của vật AB nằm giữa trung tâm thấu kính và vật nên a'b' sẽ được phóng đại so với vật AB ban đầu. Ta có thể sử dụng quy tắc nhận diện ảnh của thấu kính hội tụ để vẽ ảnh.
Theo đó:
Vật AB đặt trước trung tâm thấu kính thì ảnh a'b' sẽ nằm sau thấu kính, có kích thước lớn hơn vật AB.Khi vật AB tiến gần đến tiêu điểm F của thấu kính (do tiệm cận vô cùng), ảnh a'b' sẽ trở thành ảnh thu nhỏ, đặt sau tiêu điểm F của thấu kính.
TM
18 tháng 4 2023
a) Bạn tự vẽ hình.
b) Hình minh họa :
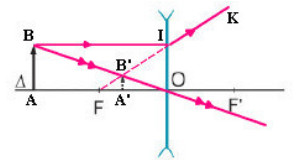
Xét \(\Delta FA'B'\sim\Delta FOI\) có : \(\dfrac{A'B'}{OI}=\dfrac{A'F}{OF}\Leftrightarrow\dfrac{A'B'}{AB}=\dfrac{OF-OA'}{OF}\)
\(\Rightarrow\dfrac{h'}{3}=\dfrac{15-d'}{15}\left(1\right)\)
Xét \(\Delta OA'B'\sim\Delta OAB\) có : \(\dfrac{A'B'}{AB}=\dfrac{OB'}{OB}\Leftrightarrow\dfrac{h'}{3}=\dfrac{d'}{30}\left(2\right)\).
Từ (1) và (2), ta có hệ phương trình : \(\left\{{}\begin{matrix}\dfrac{h'}{3}=\dfrac{15-d'}{15}\\\dfrac{h'}{3}=\dfrac{d'}{30}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}d'=10\left(cm\right)\\h'=1\left(cm\right)\end{matrix}\right.\).
Vậy : Ảnh A'B' cách thấu kính \(d'=10\left(cm\right)\) và cao \(h'=1\left(cm\right)\).
14 tháng 4 2022
Ảnh ảo, cùng chiều và lớn hơn vật.
Ảnh cách thấu kính một đoạn:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{10}=\dfrac{1}{15}+\dfrac{1}{d'}\Rightarrow d'=30cm\)
Chiều cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{3}{h'}=\dfrac{15}{30}\Rightarrow h'=6cm\)