Giải dùm tooi vs
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
3.
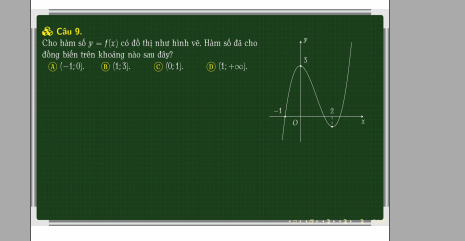
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
B đúng
4.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
A đúng
1.
B sai (thiếu điều kiện \(f'\left(x\right)=0\) tại hữu hạn điểm)
MT
3
DT
Đỗ Thanh Hải
CTVVIP
13 tháng 5 2021
1 were
2 was
3 Were
4 was
5 was
6 was
7 was
B
1 John could play the piano when he was 6
2 My brother could draw beautiful picture when he was seven
3 We could speak 2 foreign languages when we were 18
4 She could dance when she was 8
5 Tiger Woods could play goft when he was 3
C
2 Could you write you name when you were 3
3 Could you read when you were 2
4 Could you count from 1 to 10 when you were 2
5 Could you talk when you were 3
6 Could you ride a bike when you were 6
7 Could you swim when you were 5
13 tháng 5 2021
A.
1. were
2. was
3. weren't
4. was
5. was
6. was
7. wasn't
B.
2. John could play the piano when he was six.
3. My brother could draw beautiful pictures when he was seven.
4. We could speak two foreign languages when we were eighteen.
5. She could dance when she was eight.
6. Tiger Woods could play golf when he was three.
C.
2. Could you write your name when you were three?
3. Could you read when you were two?
4. Could you count from one to ten when you were two?
5. Could you talk when your were three?
6. Could you ride a bike when you were six?
7. Could you swim when you were five?
1 tháng 10 2021
\(1,\\ a,=3x\left(1-3y\right)\\ b,=9xy\left(2xy-x^2+4y\right)\\ c,=\left(x-y\right)\left(15x-5y\right)=5\left(x-y\right)\left(3x-y\right)\\ 2,\\ a,\Rightarrow2x^2\left(x^2-4\right)=0\Rightarrow2x^2\left(x-2\right)\left(x+2\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\\ b,\Rightarrow\dfrac{2}{5}x\left(x+10\right)-\left(x+10\right)=0\\ \Rightarrow\left(x+10\right)\left(\dfrac{2}{5}x-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=-10\\\dfrac{2}{5}x=1\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-10\\x=\dfrac{5}{2}\end{matrix}\right.\)
\(3,\)
\(a,\left\{{}\begin{matrix}AK=KD\\BI=IC\end{matrix}\right.\Rightarrow KI\) là đtb hình thang ABCD
\(b,\) Vì KI là đtb hình thang ABCD nên \(KI=\dfrac{AB+CD}{2}=\dfrac{17}{2}=8,5\left(cm\right)\)
\(c,\) \(\left\{{}\begin{matrix}AK=KD\\KE//AB\end{matrix}\right.\Rightarrow BE=ED\Rightarrow KE\) là đtb tam giác ABD
\(\Rightarrow KE=\dfrac{1}{2}AB=2,5\left(cm\right)\)
\(\left\{{}\begin{matrix}BI=IC\\IF//AB\end{matrix}\right.\Rightarrow AF=FC\Rightarrow IF\) là đtb tam giác ABC
\(\Rightarrow IF=\dfrac{1}{2}AB=2,5\left(cm\right)\)
Ta có \(EF=KI-KE-IF=8,5-2,5-2,5=3,5\left(cm\right)\)
TP
11 tháng 5 2022
\(a.Fe+2HCl\rightarrow FeCl_2+H_2\\ b.n_{Fe}=0,15\left(mol\right)\\ n_{HCl\left(pứ\right)}=2n_{Fe}=0,3\left(mol\right)\\ \Rightarrow m_{HCl\left(pứ\right)}=0,3.36,5=10,95\left(g\right)\\ \Rightarrow m_{ddHClpu}=\dfrac{10,95}{10,95\%}=100\left(g\right)\\ Dùngdư10gddHCl\\ \Rightarrow m_{HCl\left(bđ\right)}=\left(100+10\right).10,95\%=12,045\left(g\right)\\ c.n_{H_2}=n_{FeCl_2}=n_{Fe}=0,15\left(mol\right)\\ m_{ddsaupu}=8,4+110-0,15.2=118,1\left(g\right)\\ C\%_{FeCl_2}=\dfrac{0,15.127}{118,1}.100=16,13\%\)
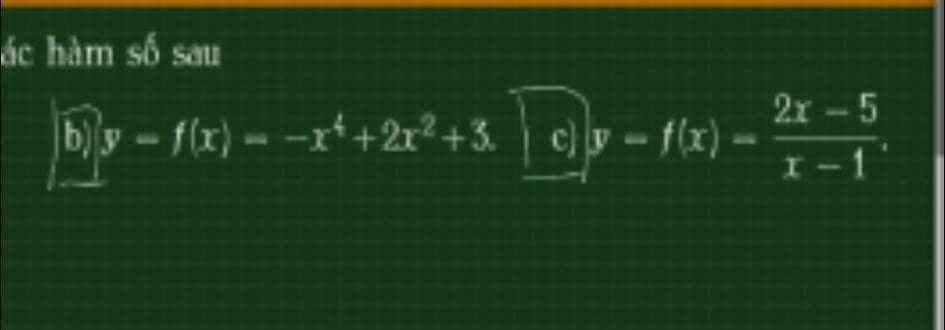
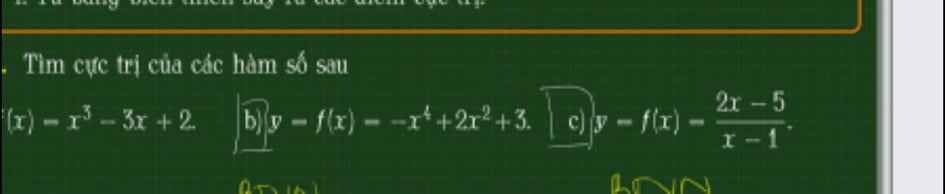
giải dùm câu 3 vs plss
a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó:ΔABH=ΔACH
Suy ra: HB=HC=BC/2=3(cm)
=>AH=4(cm)
a. Vì AH là đường cao
=> AH ⊥ BC (H ∈ BC)
=> góc AHB = góc AHC = 90o
Vì △ ABC cân tại A
=> AB = AC
Xét △ABH và △ACH:
AB = AC (cmt)
góc AHB = góc AHC = 90o
AH chung
=> △ABH = △ACH (cgv-ch) (đpcm)
=> BH = CH (2 cạnh tương ứng)
=> BH = CH = \(\dfrac{BC}{2}=\dfrac{6}{2}=3\left(cm\right)\)
Áp dụng định lí Pi-ta-go vào tam giác ABH:
AB2 = AH2 + BH2
52 = AH2 + 32
25 = AH2 + 9
AH2 = 25 - 9 = 16
=> AH = 4 (cm)
b. thiếu câu hỏi nhé bạn .-.