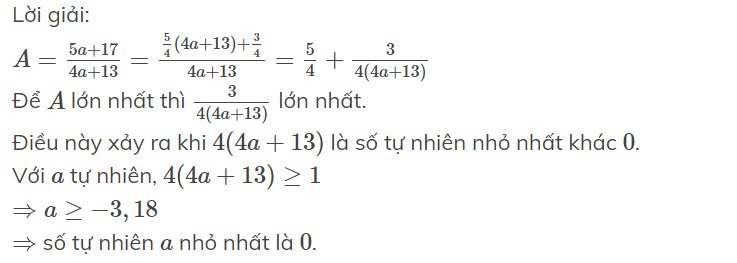TÌM GIÁ TRỊ LỚN NHẤT CỦA (5a+17) / (4a+13)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$\frac{5a+17}{4a+13}=\frac{\frac{5}{4}(4a+13)+\frac{3}{4}}{4a+13}$
$=\frac{5}{4}+\frac{3}{4(4a+13)}$
Để phân số trên max thì $\frac{3}{4(4a+13)}$ max
Điều này xảy ra khi $4a+13$ là số nguyên dương nhỏ nhất.
Với $a$ là stn, $4a+13$ là số nguyên dương nhỏ nhất khi $a$ nhỏ nhất, bằng $0$
Vậy $a=0$

Lời giải:
\(A=\frac{5a+17}{4a+13}=\frac{\frac{5}{4}(4a+13)+\frac{3}{4}}{4a+13}=\frac{5}{4}+\frac{3}{4(4a+13)}\)
Để $A$ lớn nhất thì $\frac{3}{4(4a+13)}$ lớn nhất.
Điều này xảy ra khi $4(4a+13)$ là số tự nhiên nhỏ nhất khác $0$.
Với $a$ tự nhiên, $4(4a+13)\geq 1$
$\Rightarrow a\geq -3,18$
$\Rightarrow$ số tự nhiên $a$ nhỏ nhất là $0$.

Bài này tớ chỉ nói thôi nhé :
Cậu phân tích phân số đó ra đc hỗn số sau đó giải thích ra hai trường hợp
TH1 : 4a + 13 > 0 suy ra 4a > -13 suy ra a > -13/4 mà a là số tự nhiên suy ra 4a + 13 > ( cậu tự tính nhé )
sau đó cậu so sánh ps trong hỗn số cậu vừa phân tích ấy vs phân số có tử giống nhau và mẫu số lần lượt là 4a + 13 và cái cậu vừa tính đc ở trên ấy
Ở trường hợp này GTLN của A là cái bạn vừa so sánh vs ps cũ + hỗn số ấy còn a là cái số tự nhiên cậu tính đc ở TH1
TH2 : 4a + 13 < 0 .............................................................................................
làm giống như trường hợp 1 chỉ là trường hợp này không có GTLN của A
Nếu cậu hiểu nhớ bấm Đúng nha
TH1 : 4a + 13 > 0 suy ra 4a > -13 suy ra a > -13/4 mà a là số tự nhiên suy ra 4a + 13 > 0
sau đó cậu so sánh ps trong hỗn số cậu vừa phân tích ấy vs phân số có tử giống nhau và mẫu số lần lượt là 4a + 13 và cái 0 ah
Ở trường hợp này GTLN của A là cái bạn vừa so sánh vs ps cũ + hỗn số ấy còn a là cái số tự nhiên cậu tính đc ở TH1
TH2 : 4a + 13 < 0 .............................................................................................?
làm giống như trường hợp 1 chỉ là trường hợp này không có GTLN của A

\(\frac{8a+19}{4a+1}=\frac{8a+2+17}{4a+1}=2+\frac{17}{4a+1}\)
để phân số trên là 1 số nguyên thì \(17⋮4a+1\)
hay \(4a+1\inƯ\left(17\right)=\left\{1;17;-1;-17\right\}\)xét :
nếu \(4a+1=1\Rightarrow4a=0\Rightarrow a=0\)
nếu \(4a+1=17\Rightarrow4a=16\Rightarrow a=4\)
nếu \(4a+1=-1\Rightarrow4a=-2\Rightarrow a=\frac{-1}{2}\) ( loại)
nếu \(4a+1=-17\Rightarrow4a=-18\Rightarrow4a=\frac{-9}{2}\) ( loại)
vây: a={0;4}
\(\frac{5a-17}{4a-23}=\frac{\frac{5}{4}\left(4a-23\right)+\frac{115}{4}-17}{4a-23}=\frac{5}{4}+\frac{47}{4\left(4a-23\right)}\)
để phân số trên có giá trị lớn nhất thì \(\frac{1}{4a-23}\) là số dương lớn nhất \(\Rightarrow4a-23\) là số nhỏ nhất mà a là số tự nhiên \(\Rightarrow4a-23=1\Rightarrow4a=24\Rightarrow a=6\)
vậy \(a=6\) thì phân số trên lớn nhất \(=\frac{5}{4}+\frac{47}{4}=\frac{52}{4}=13\)

\(A=\frac{5a-17}{4a-23}=\frac{\frac{5}{4}.\left(4a-23\right)+\frac{115}{4}-17}{4a-23}=\frac{5}{4}+\frac{47}{4.\left(4a-23\right)}\)
Để A lớn nhất thì \(\frac{1}{4a-23}\) là số dương lớn nhất => 4a - 23 là nhỏ nhất mà a là số tự nhiên => 4a - 23 =1 => a = 6
Vậy a = 6 thì A lớn nhất bằng \(\frac{5}{4}+\frac{47}{4}=\frac{52}{4}=13\)