Hình thoi có 1710 cm2 ,tính cạnh hình thoi biết 1 canh là 45 cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


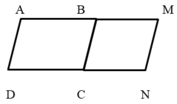
Vì hình ABCD là hình bình hành nên cạnh AD = BC = 3cm. Vì hình BMNC là hình thoi nên có các cạnh bằng nhau, do đó ta có :
BC = BM = MN = 3 cm
Chiều cao tương ứng cạnh DC của hình bình hành ABCD là :
8 : 4 = 2 (cm)
Chiều cao tương ứng cạnh DC cũng là chiều cao tương ứng cạnh NC do đó diện tích hình thoi BMNC là :
3 x 2 = 6 (cm2)
Đáp số : 6 cm2
Vì hình ABCD là hình bình hành nên cạnh AD = BC = 3cm. Vì hình BMNC là hình thoi nên có các cạnh bằng nhau, do đó ta có :
BC = BM = MN = 3 cm
Chiều cao tương ứng cạnh DC của hình bình hành ABCD là :
8 : 4 = 2 (cm)
Chiều cao tương ứng cạnh DC cũng là chiều cao tương ứng cạnh NC do đó diện tích hình thoi BMNC là :
3 x 2 = 6 (cm2) Đáp số:6 cm2

Vì hình ABCD là hình bình hành nên cạnh AD = BC = 3cm. Vì hình BMNC là hình thoi nên có các cạnh bằng nhau, do đó ta có: BC = BM = MN = 3 cm Chiều cao tương ứng cạnh DC của hình bình hành ABCD là: 8 : 4 = 2 (cm) Chiều cao tương ứng cạnh DC cũng là chiều cao tương ứng cạnh NC do đó diện tích hình thoi BMNC là : 3 x 2 = 6 (cm2 ) Đáp số: 6 cm2

1. Gọi I chính là giao điểm của BD và AC. Ta có: AB = BC = DC = AD = AH + BH = 7+2 = 9(cm)
Xét\(\Delta AHD\left(\widehat{AHD}=90^0\right)\) theo định lý py - ta - go ta có :
\(HD=\sqrt{AD^2-AH^2}=\sqrt{9^2-7^2}=4\sqrt{2}cm\)
Xét\(\Delta BHD\left(\widehat{BHD=90^O}\right)\)theo định lý py - ta - go ta có :
\(BD=\sqrt{HD^2+BH^2}=\sqrt{\left(4\sqrt{2}\right)^2+2^2}=6cm\)
BI = DI =\(\frac{BD}{2}=\frac{6}{2}=3cm\). Xét\(\Delta AID\left(\widehat{AID}=90^O\right)\)theo định lý py - ta - go ta có :
\(AI=\sqrt{AD^2-DI^2}=\sqrt{9^2-3^2}=6\sqrt{2cm}\)
AC = AI.2 =\(6\sqrt{2}.2=12\sqrt{2}\)=> SABCD =\(\frac{1}{2}.\left(BD.AC\right)=\frac{1}{2}.\left(6.12\sqrt{2}\right)=36\sqrt{2}cm\)

Đổi 10m = 1000cm
Độ dài thu nhỏ cạnh hình thoi là:
1000 : 500 = 2 (cm)
Đáp số: 2cm

Bài giải:
Cạnh 2 của hình thoi là:
1710 x 2 : 45 = 76 (cm)
Đáp số: 76cm.