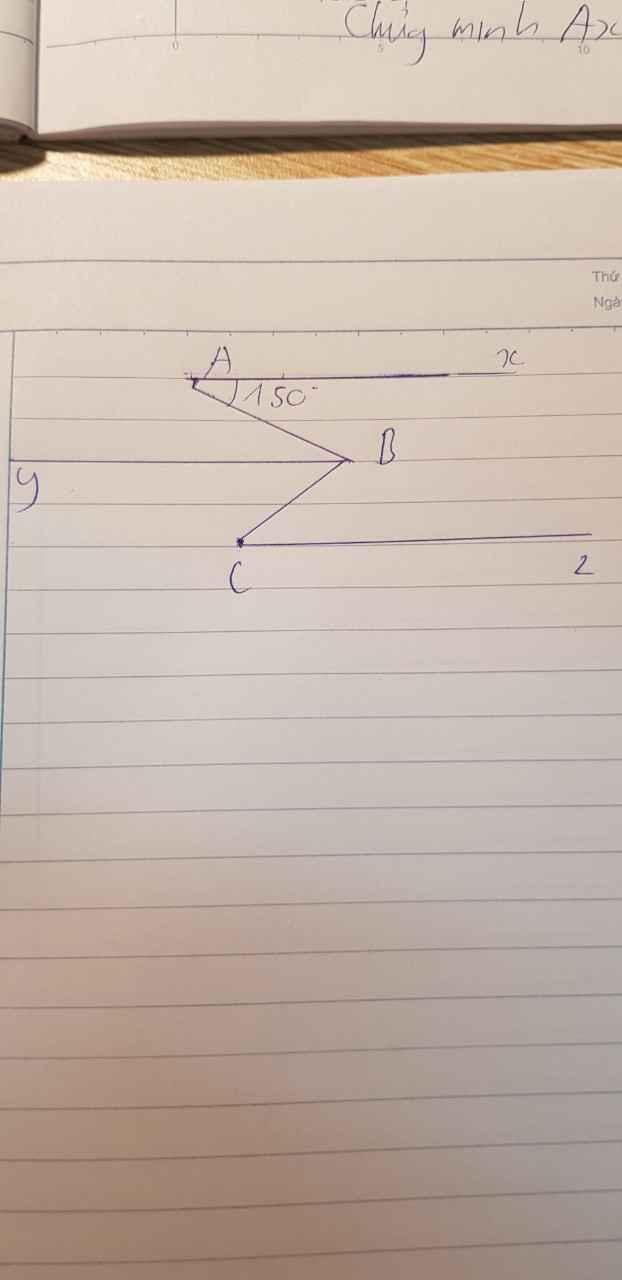
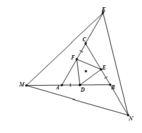
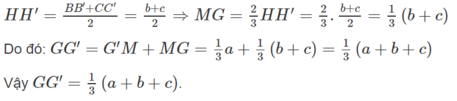Cho tam giác ABC gọi Ax, By, Cz lần lượt là các tia AB,BC,CA . Tính CAx +ABy+BCz ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét tam giác ABC có:
\(A_1+B_1+C_1=180^o\)
Mà Ã;By;CZ lần lượt là các tia đối của AB;BC;CA nên
\(\text{CAx + ABy + BCx}=C_1+A_1+B_1=180^o\)

Bài này không khó,chỉ dùng kiến thức về song song(các góc sole trong,...)
Cái này thì mình thấy chắc suy ra trực tiếp luôn


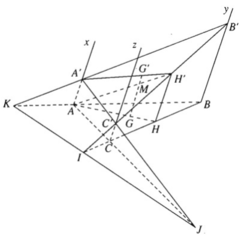
a) CC′ // BB′ ⇒ ΔICC′ ∼ ΔIBB′
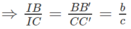
CC′ // AA′ ⇒ ΔJCC′ ∼ ΔJAA′
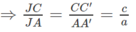
AA′ // BB′ ⇒ ΔKAA′ ∼ ΔKBB′
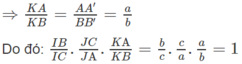
b) Gọi H và H’ lần lượt là trung điểm của các cạnh BC và B’C’. Vì HH’ là đường trung bình của hình thang BB’CC’ nên HH′ // BB′.
Mà BB′ // AA′ suy ra HH′ // AA′
Ta có: G ∈ AH và G′ ∈ A′H′ và ta có:
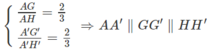
c) AH′ ∩ GG′ = M ⇒ GG′ = G′M + MG
Ta có: G′M // AA′ ⇒ ΔH′G′M ∼ ΔH′A′A
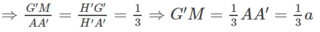
MG // HH′ ⇒ ΔAMG ∼ ΔAH′H
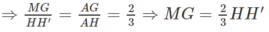
Mặt khác HH’ là đường trung bình của hình thang BB’CC’ nên