Cho hàm số y= ax2 (P) đi qua điểm A(1;2)
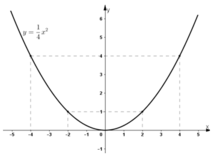
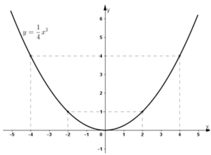
a) xác định a và vẽ đồ thị
b) cho đường thẳng y =-x+b cắt (P) tại A và B. Xác định b và tính toạ độ B
c) cho đường thẳng (d): y= mx-m2-\(\dfrac{3}{2}m-\dfrac{3}{4}\) . chứng minh (d) và (P) không cắt nhau với mọi m

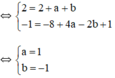
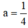
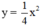
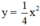
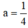
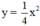
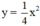


giải câu c là dc rùi nha
(P): \(y=2x^2\)
Phương trình hoành độ giao điểm (P) và (d):
\(2x^2=mx-m^2-\dfrac{3}{2}m-\dfrac{3}{4}\)
\(\Leftrightarrow2x^2-mx+m^2+\dfrac{3}{2}m+\dfrac{3}{4}=0\) (1)
\(\Delta=m^2-8\left(m^2+\dfrac{3}{2}m+\dfrac{3}{4}\right)=-7m^2-12m-6=-7\left(m+\dfrac{6}{7}\right)^2-\dfrac{6}{7}< 0\) ; \(\forall m\)
\(\Rightarrow\) (1) vô nghiệm với mọi m hau (d) và (P) ko cắt nhau với mọi m