Cho \(x\ge2\)CM: \(x^3+4x^2-3x-18\ge0\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Thay x=2 vào biểu thức
\(x^3+4x^2-3x-18=2^3+4.2^2-3.2-18=8+16-6-18=0\)
Do x=2 cho ta \(x^3+4x^2-3x-18=0\) nên với mọi x lớn hơn hoặc bằng 2 ta luôn thu đc biểu thức lớn hơn hoặc bằng 0
\(x^3+4x^2-3x-18\ge0\)
\(\Leftrightarrow x^3+6x^2+9x-2x^2-12x-18\ge0\)
\(\Leftrightarrow x\left(x^2+6x+9\right)-2\left(x^2+6x+9\right)\ge0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2+6x+9\right)\ge0\)
\(\Leftrightarrow\left(x-2\right)\left(x+3\right)^2\ge0\)
Từ \(\left\{{}\begin{matrix}x\ge2\Rightarrow x-2\ge0\\\left(x+3\right)^2\ge0\end{matrix}\right.\)
\(\Rightarrow\left(x-2\right)\left(x+3\right)^2\ge0\forall x\ge2\) (Đúng !!)

Ta có :x+y\(\ge2\sqrt{xy}\)
\(\Leftrightarrow\left(\sqrt{x}\right)^2+\left(\sqrt{y}\right)^2+2\sqrt{x}\sqrt{y}\ge0\)
\(\Leftrightarrow\left(\sqrt{x}-\sqrt{y}\right)^2\ge0\)(luôn đúng với mọi x,y\(\ge0\))
Dấu"+" xảy ra khi:\(\sqrt{x}=\sqrt{y}\Leftrightarrow x=y\)
Vậy với mọi x,y\(\ge0\) thì x+y\(\ge2\sqrt{xy}\)
đong 2 bạn đổi lại dấu +\(2\sqrt{xy}\) thành -\(2\sqrt{xy}\) giùm mình

a. TH1:
\(\left\{{}\begin{matrix}x^2+3x-4< 0\\3-2x>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x< 1\\x>-4\end{matrix}\right.\\x>\dfrac{3}{2}\end{matrix}\right.\)
TH2:
\(\left\{{}\begin{matrix}x^2+3x-4>0\\3-2x< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x>1\\x< -4\end{matrix}\right.\\x< \dfrac{3}{2}\end{matrix}\right.\)
Vậy nghiệm của BPT:
\(\left\{{}\begin{matrix}\left[{}\begin{matrix}x< 1\\x>-4\end{matrix}\right.\\x>\dfrac{3}{2}\end{matrix}\right.\) \(\left\{{}\begin{matrix}\left[{}\begin{matrix}x>1\\x< -4\end{matrix}\right.\\x< \dfrac{3}{2}\end{matrix}\right.\)

ĐK: \(x\ge4;x\le0\)
TH1: \(\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\Rightarrow bpt\) đúng
TH2: \(x\ne0;x\ne4\)
Bất phương trình tương đương:
\(\dfrac{x^2-3x+2}{x-3}\ge0\)
\(\Leftrightarrow\dfrac{\left(x-1\right)\left(x-2\right)}{x-3}\ge0\)
Lập bảng xét dấu:
Dựa vào bảng xét dấu, bất phương trình có nghiệm \(x\in\left[1;2\right]\cup\left(3;+\infty\right)\)
Kết luận: Bất phương trình đã cho có tập nghiệm \(x\in\left[1;2\right]\cup\left(3;+\infty\right)\cup\left\{0\right\}\)
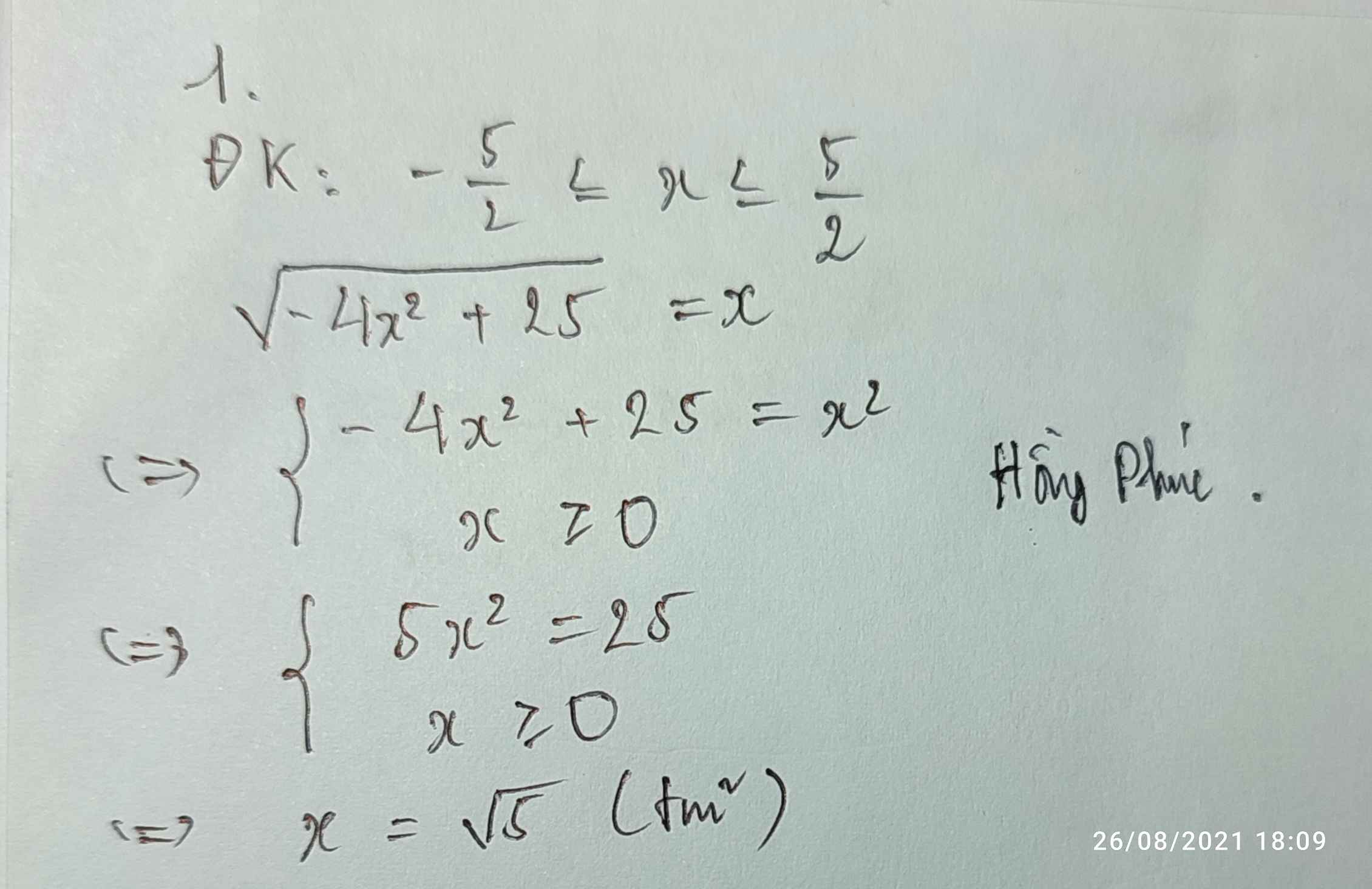
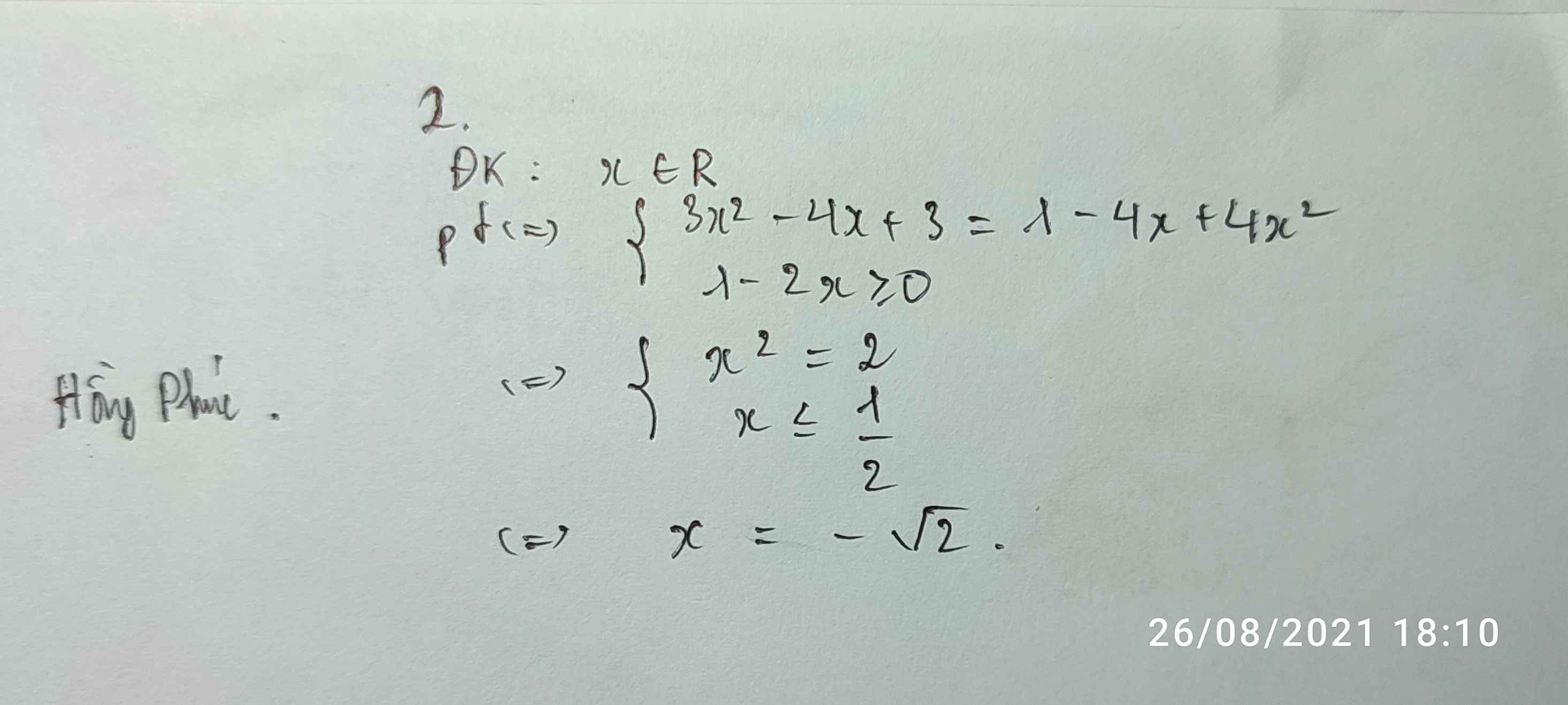
x3+4x2-3x-18
Q(x)=x3+4x2-3x-18
Ta thấy: Q(-2)=(-2)3+4*(-2)2-3*(-2)-18=0
Nên chia Q cho x-2 ta được:
=(x-2)(x2+6x+9)
=(x-2)(x+3)2\(\ge\)0 với mọi x\(\ge\)2