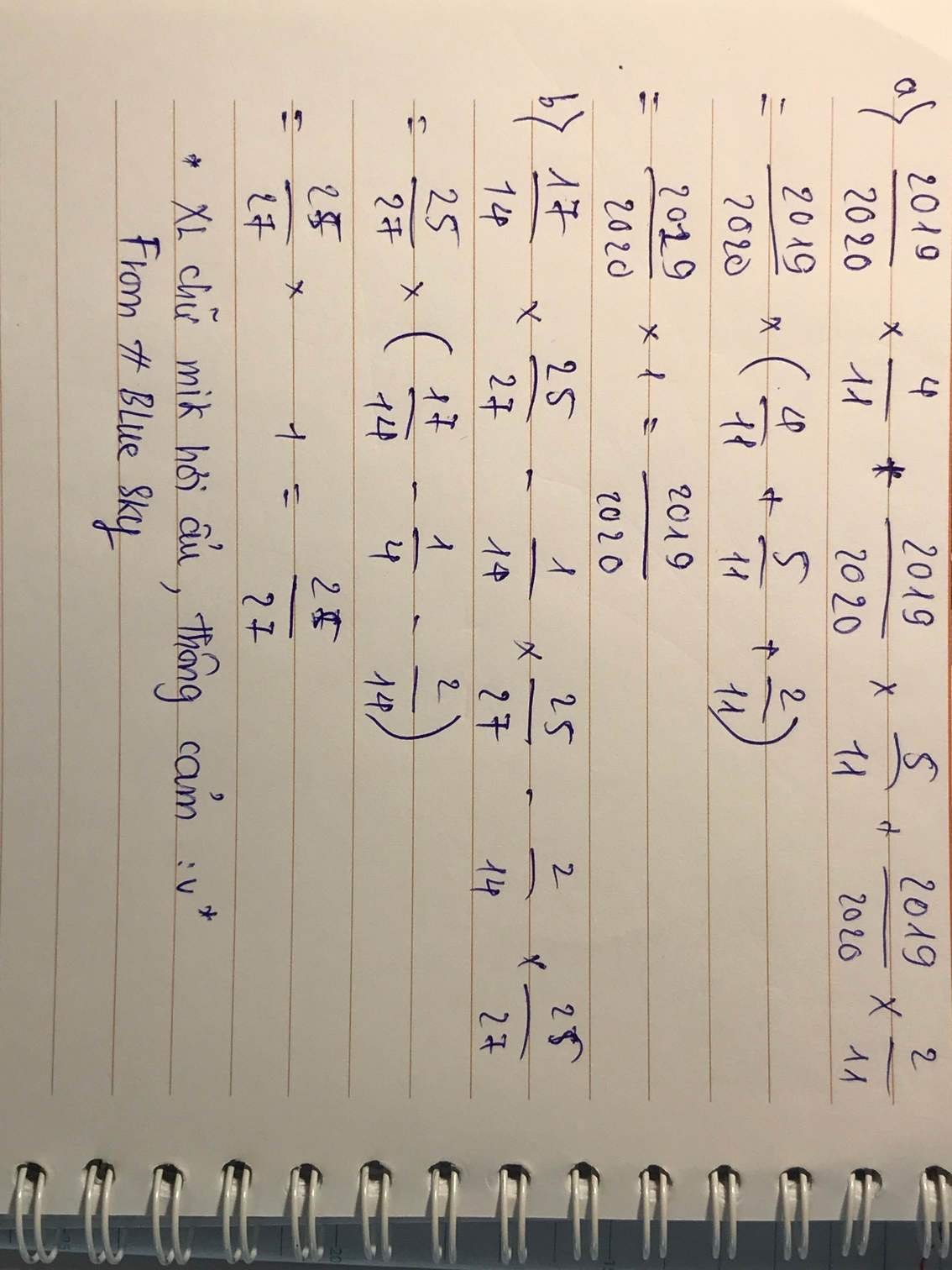2019/2020 x 7/8+2019/2020 x3/8-2019/2020 x1/4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 6 2023
a: \(A=1-\dfrac{2\left(25-\dfrac{2}{2018}+\dfrac{1}{2019}-\dfrac{1}{2020}\right)}{4\left(25-\dfrac{2}{2018}+\dfrac{1}{2019}-\dfrac{1}{2020}\right)}\)
=1-2/4=1/2
b: \(B=\dfrac{5^{10}\cdot7^3-5^{10}\cdot7^4}{5^9\cdot7^3+5^9\cdot7^3\cdot2^3}\)
\(=\dfrac{5^{10}\cdot7^3\left(1-7\right)}{5^9\cdot7^3\left(1+2^3\right)}=5\cdot\dfrac{-6}{9}=-\dfrac{10}{3}\)
c: x-y=0 nên x=y
\(C=x^{2020}-x^{2020}+y\cdot y^{2019}-y^{2019}\cdot y+2019\)
=2019
NH
3
H
19 tháng 5 2021
1. \(\dfrac{2019}{2020}-\left(\dfrac{2019}{2020}-\dfrac{2020}{2021}\right)\)
\(=\dfrac{2019}{2020}-\dfrac{2019}{2020}+\dfrac{2020}{2021}\)
\(=0+\dfrac{2020}{2021}=\dfrac{2020}{2021}\)
19 tháng 5 2021
Giải:
1) \(\dfrac{2019}{2020}-\left(\dfrac{2019}{2020}-\dfrac{2020}{2021}\right)\)
\(=\dfrac{2019}{2020}-\dfrac{2019}{2020}+\dfrac{2020}{2021}\)
\(=\left(\dfrac{2019}{2020}-\dfrac{2019}{2020}\right)+\dfrac{2020}{2021}\)
\(=0+\dfrac{2020}{2021}\)
\(=\dfrac{2020}{2021}\)
2) \(\dfrac{2}{9}+\dfrac{7}{9}:\left(\dfrac{42}{5}-\dfrac{7}{5}\right)\)
\(=\dfrac{2}{9}+\dfrac{7}{9}:7\)
\(=\dfrac{2}{9}+\dfrac{1}{9}\)
\(=\dfrac{1}{3}\)
3) \(\dfrac{3}{4}+\dfrac{x}{4}=\dfrac{5}{8}\)
\(\dfrac{x}{4}=\dfrac{5}{8}-\dfrac{3}{4}\)
\(\dfrac{x}{4}=\dfrac{-1}{8}\)
\(\Rightarrow x=\dfrac{4.-1}{8}=\dfrac{-1}{2}\)
4) \(\left|3x+1\right|-\dfrac{1}{4}=\dfrac{-1}{4}\)
\(\left|3x-1\right|=\dfrac{-1}{4}+\dfrac{1}{4}\)
\(\left|3x-1\right|=0\)
\(3x-1=0\)
\(3x=0+1\)
\(3x=1\)
\(x=1:3\)
\(x=\dfrac{1}{3}\)
Chúc bạn học tốt!
PK
2
24 tháng 3 2019
c) \(M=\frac{2019}{2020}+\frac{2020}{2021}\) và \(N=\frac{2019+2020}{2020+2021}\)
Ta có \(\frac{2019}{2020}>\frac{2019}{2020+2021}\)
\(\frac{2020}{2021}>\frac{2020}{2020+2021}\)
\(\Rightarrow\frac{2019}{2020}+\frac{2020}{2021}< \frac{2019+2020}{2020+2021}=N\)
\(\Rightarrow M>N\)
31 tháng 10 2020
\(\left(8^{2020}+8^{2019}\right):8^{2019}\)
\(=\frac{8^{2020}+8^{2019}}{8^{2019}}\)
\(=\frac{8^{2019}\cdot\left(8^1+1\right)}{8^{2019}}\)
\(=8^1+1\)
\(=8+1\)
\(=9\)
K
1
28 tháng 6 2021
Ta có: \(A=\left(2020^{2019}+2019^{2019}\right)^{2020}\)
\(=\left(2019^{2019}+2020^{2019}\right)^{2019}\cdot\left(2019^{2019}+2020^{2019}\right)\)
\(\Leftrightarrow\dfrac{A}{B}=\dfrac{\left(2019^{2019}+2020^{2019}\right)^{2019}\cdot\left(2019^{2019}+2020^{2019}\right)}{\left(2020^{2020}+2019^{2020}\right)^{2019}}\)
\(\Leftrightarrow\dfrac{A}{B}=\dfrac{2019^{2019}+2020^{2019}}{2019+2020}>1\)
\(\Leftrightarrow A>B\)
1 tháng 12 2023
\(A=\dfrac{2020^{2018}-1}{2020^{2019}+2019}\)
\(B=\dfrac{2020^{2019}+1}{2020^{2020}+2019}\)
Ta có :
\(A-B=\dfrac{2020^{2018}-1}{2020^{2019}+2019}-\dfrac{2020^{2019}+1}{2020^{2020}+2019}\)
\(\Rightarrow A-B=\dfrac{\left(2020^{2018}-1\right)\left(2020^{2020}+2019\right)-\left(2020^{2019}+2019\right)\left(2020^{2019}+1\right)}{\left(2020^{2019}+2019\right)\left(2020^{2020}+2019\right)}\)
\(\Rightarrow A-B=\dfrac{2020^{4038}+2019.2020^{2018}-2020^{2020}-2019-2020^{4038}-2020^{2019}-2019.2020^{2018}-2029}{\left(2020^{2019}+2019\right)\left(2020^{2020}+2019\right)}\)
\(\Rightarrow A-B=\dfrac{-\left(2020^{2020}+2020^{2019}+2.2019\right)}{\left(2020^{2019}+2019\right)\left(2020^{2020}+2019\right)}\)
mà \(\left\{{}\begin{matrix}-\left(2020^{2020}+2020^{2019}+2.2019\right)< 0\\\left(2020^{2019}+2019\right)\left(2020^{2020}+2019\right)>0\end{matrix}\right.\)
\(\Rightarrow A-B< 0\)
\(\Rightarrow A< B\)
Vậy ta được \(A< B\)
NA
12 tháng 3 2022
\(a.=\dfrac{2019}{2020}\times\left(\dfrac{4}{11}+\dfrac{5}{11}+\dfrac{2}{11}\right)\\ =\dfrac{2019}{2020}\times1=\dfrac{2019}{2020}\\ b.=\dfrac{25}{27}\times\left(\dfrac{17}{14}-\dfrac{1}{14}-\dfrac{2}{14}\right)\\ =\dfrac{25}{27}\times1=\dfrac{25}{27}\)