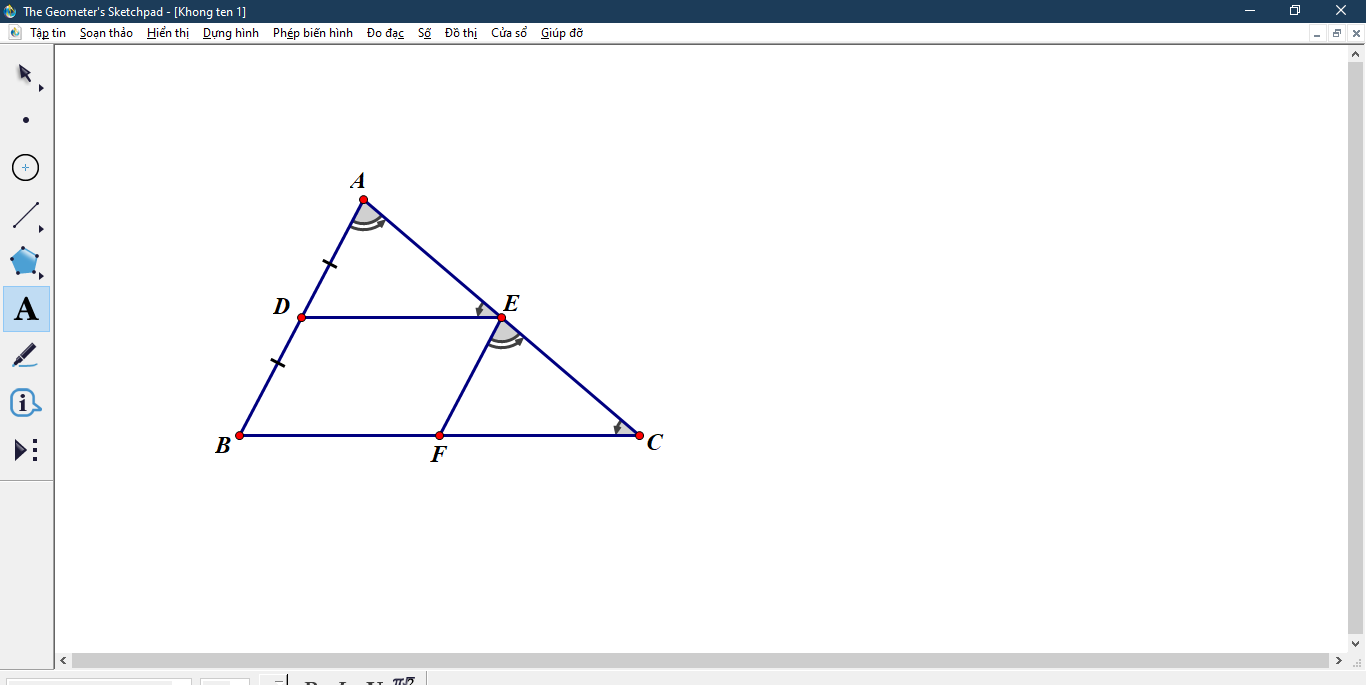
Cho tam giác ABC điểm D nằm giữa B và C qua D vẽ đg thẳng song song với AB cắt AC ở P qua D vẽ dg thẳng song song với AC cắt AB ở Q gọi I là trung điểm của AD
a) Cm P,Q đois xứng nhau qua I
b) Tam giắc ABC có điều kiện gì thì tứ giác APDQ là hình chữ nhật