Cho ΔABC cân (AB=AC). Các đường phân giác BE,CF cắt nhau tại H.
a. Chứng minh ΔABE = ΔACF
b. Tia AH cắt BC tại D. Chứng minh D là trung điểm của BC và EF song song với BC
c. Chứng minh AH là trung trực của EF. So sánh HF và HC
d. Tìm điều kiện của ΔABC để HC = 2.HD

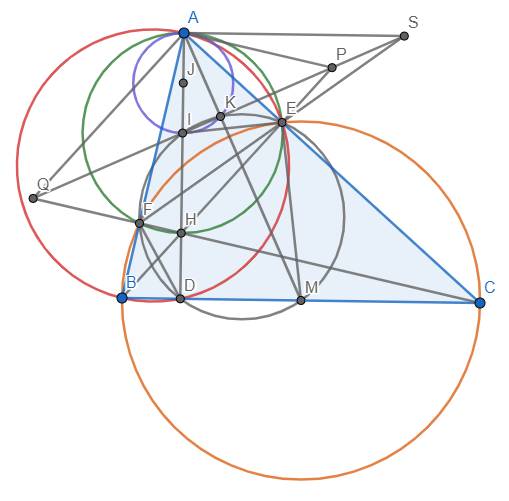

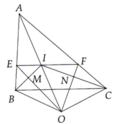






a: Xét ΔABE và ΔACF có
\(\widehat{ABE}=\widehat{ACF}\)
AB=AC
góc A chung
Do đó: ΔABE=ΔACF
b: Xét ΔHBC có \(\widehat{HBC}=\widehat{HCB}\)
nên ΔHBC cân tại H
=>HB=HC
mà AB=AC
nên AH là đường trung trực của BC
=>D là trung điểm của BC
Xét ΔABC có AF/AB=AE/AC
nên EF//BC