Giúp mình từ bài 26 đến hết ạh
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
26 tháng 10 2023
Lời giải:
1.
$x^3+3x^2-16x-48=(x^3+3x^2)-(16x+48)=x^2(x+3)-16(x+3)$
$=(x+3)(x^2-16)=(x+3)(x-4)(x+4)$
2.
$4x(x-3y)+12y(3y-x)=4x(x-3y)-12y(x-3y)=(x-3y)(4x-12y)=4(x-3y)(x-3y)=4(x-3y)^2$
3.
$x^3+2x^2-2x-1=(x^3-x^2)+(3x^2-3x)+(x-1)=x^2(x-1)+3x(x-1)+(x-1)$
$=(x-1)(x^2+3x+1)$
NV
2
16 tháng 7 2021
III:
1) \(x-y=\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)\)
2) \(x-1=\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)\)
4) \(a-2\sqrt{a}+1=\left(\sqrt{a}-1\right)^2\)
5) \(2x-\sqrt{x}-3=\left(\sqrt{x}+1\right)\left(2\sqrt{x}-3\right)\)
6) \(6a^2-5a\sqrt{b}-b=\left(a-\sqrt{b}\right)\left(6a+\sqrt{b}\right)\)
7) \(x-2\sqrt{x-1}-y^2=\left(\sqrt{x-1}-1\right)^2-y^2=\left(\sqrt{x-1}-1-y\right)\left(\sqrt{x-1}-1+y\right)\)
16 tháng 7 2021
II:
2.8) ĐKXĐ: \(x\ge2\)
2.9: ĐKXĐ: \(\left[{}\begin{matrix}x< \dfrac{1}{2}\\\dfrac{1}{2}< x\le1\end{matrix}\right.\)
2.10: ĐKXĐ: \(x\ne0\)
2.11: ĐKXĐ: \(\left[{}\begin{matrix}x\le-5\\x\ge3\end{matrix}\right.\)
3 tháng 10 2023
26 It was silly to lend him money
27 Meeting the president is exciting
28 While we were in the summer holiday, we were happy
29 While the play was being played, they cried twice
30 Writing good compositions in English was not easy
SV
Sinh Viên NEU
CTVVIP
6 tháng 10 2023
1 It was silly to lend him money
2 Meeting the president is exciting
3 While we were on the summer holiday, we were so happy
4 While they were playing, they cried twice
5 Writing good composition in English was not easy
NV
10
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 3 2021
18.
Áp dụng BĐT quen thuộc: \(\dfrac{1}{1+x^2}+\dfrac{1}{1+y^2}\ge\dfrac{2}{1+xy}\) ta có:
\(\dfrac{1}{1+a^3}+\dfrac{1}{1+b^3}\ge\dfrac{2}{1+\sqrt{a^3b^3}}\) ; \(\dfrac{1}{1+c^3}+\dfrac{1}{1+abc}\ge\dfrac{2}{1+\sqrt{abc^4}}\)
Cộng vế:
\(\dfrac{1}{1+a^3}+\dfrac{1}{1+b^3}+\dfrac{1}{1+c^3}+\dfrac{1}{1+abc}\ge2\left(\dfrac{1}{1+\sqrt{a^3b^3}}+\dfrac{1}{1+\sqrt{abc^4}}\right)\ge2\left(\dfrac{2}{1+\sqrt[4]{a^4b^4c^4}}\right)\)
\(\Rightarrow\dfrac{1}{1+a^3}+\dfrac{1}{1+b^3}+\dfrac{1}{1+c^3}+\dfrac{1}{1+abc}\ge\dfrac{4}{1+abc}\)
\(\Rightarrow\dfrac{1}{1+a^3}+\dfrac{1}{1+b^3}+\dfrac{1}{1+c^3}\ge\dfrac{3}{1+abc}\) (đpcm)
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 3 2021
19.
Biến đổi tương đương:
\(\Leftrightarrow\left(a^2+b^2\right)xy+ab\left(x^2+y^2\right)\ge\left(a^2+b^2+2ab\right)xy\)
\(\Leftrightarrow\left(a^2+b^2\right)xy+ab\left(x^2+y^2\right)\ge\left(a^2+b^2\right)xy+2abxy\)
\(\Leftrightarrow ab\left(x^2+y^2\right)-2abxy\ge0\)
\(\Leftrightarrow ab\left(x^2+y^2-2xy\right)\ge0\)
\(\Leftrightarrow ab\left(x-y\right)^2\ge0\)
1 tháng 8 2023
Ta có :
\(AH^2=AB^2+BH^2\left(1\right)\) (Δ ABH vuông tại H)
\(AH^2=AC^2+CH^2\left(2\right)\) (Δ ACH vuông tại H)
\(\left(1\right),\left(2\right)\Rightarrow AB^2+BH^2=AC^2+CH^2\)
\(\Rightarrow CH^2=AB^2+BH^2-AC^2\)
\(\Rightarrow CH^2=81+676-121=636\)
\(\Rightarrow CH=\sqrt[]{636}=\sqrt[]{4.159}=2\sqrt[]{159}\left(cm\right)\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
31 tháng 7 2023
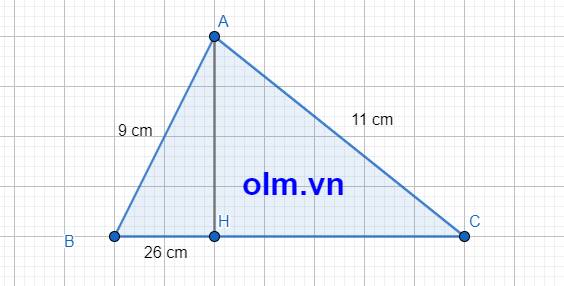
Vì AH là đường cao của tam giác ABC nên AH \(\perp\) BC \(\equiv\) H
⇒ \(\Delta\) AHB \(\perp\) \(\equiv\) H \(\Rightarrow\) AB > BH ⇒ 9 cm > 26 cm vô lý
Em có hai sựa lựa chọn: 1 là em chỉ ra cái sai của cô
2 là em xem lại đề bài của em
Bài 26:
Độ dài đường kính của hình tròn đó là:
24 × 2 = 48 ( cm )
Bài 27 :
Độ dài bán kính của hình tròn đó là:
48 ÷ 2 = 24 ( cm )
Bài 28
Độ dài bán kính hình tròn đó là :
96 ÷ 2 = 48 ( cm )