Cho hàm số y = f(x) = x2 + 4x + 3 có đồ thị như hình vẽ:
Tìm m để: x2 + 4x +2m + 1 = 0 có 2 nghiệm âm phân biệt
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn kiểm tra đồ thị giúp mình, nhầm đồ thị rồi!
x2+4x+m-3=0 \(\Leftrightarrow\) x2+4x+3=6-m.
f(-3)=0.
Ycđb \(\Leftrightarrow\) 6-m>0 \(\Rightarrow\) m<6.

Bài 1:
\(c,\text{PT có 2 }n_0\text{ phân biệt }\Leftrightarrow\Delta'=2^2-2m>0\Leftrightarrow2m< 4\Leftrightarrow m< 2\)

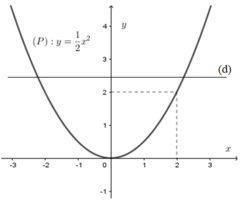
Xét phương trình x2 – 2m + 4 = 0 (*)
⇔ x2 = 2m – 4 ⇔ 1 2 x 2 = m − 2
Số nghiệm của phương trình (*) là
số giao điểm của parabol (P): y = 1 2 x 2
và đường thẳng d: y = m – 2
Để (*) có hai nghiệm phân biệt thì d cắt (P) tại hai điểm phân biệt
Từ đồ thị hàm số ta thấy:
Với m – 2 > 0 ⇔ m > 2 thì d cắt (P)
tại hai điểm phân biệt hay phương trình (*)
có hai nghiệm phân biệt khi m > 2
Đáp án cần chọn là: A
x2+4x+2m+1=0 \(\Leftrightarrow\) x2+4x+3=-2m+2.
Phương trình đã cho có tối đa một nghiệm âm, xảy ra khi -2m+2>3.
Vậy không có giá trị nào của m thỏa yêu cầu đề bài.
Xin lỗi! Mình bất cẩn, bạn kiểm tra lại đồ thị giúp mình, bạn nhầm đồ thị rồi!
Giải:
x2+4x+2m+1=0 ⇔ x2+4x+3=-2m+2.
f(0)=3.
Ycđb \(\Leftrightarrow\) -1<-2m+2<3 \(\Rightarrow\) -1/2<m<3/2.