Mọi ng giải mik câu(d) bài 11 và các câu của Bài 15 đc ko ạ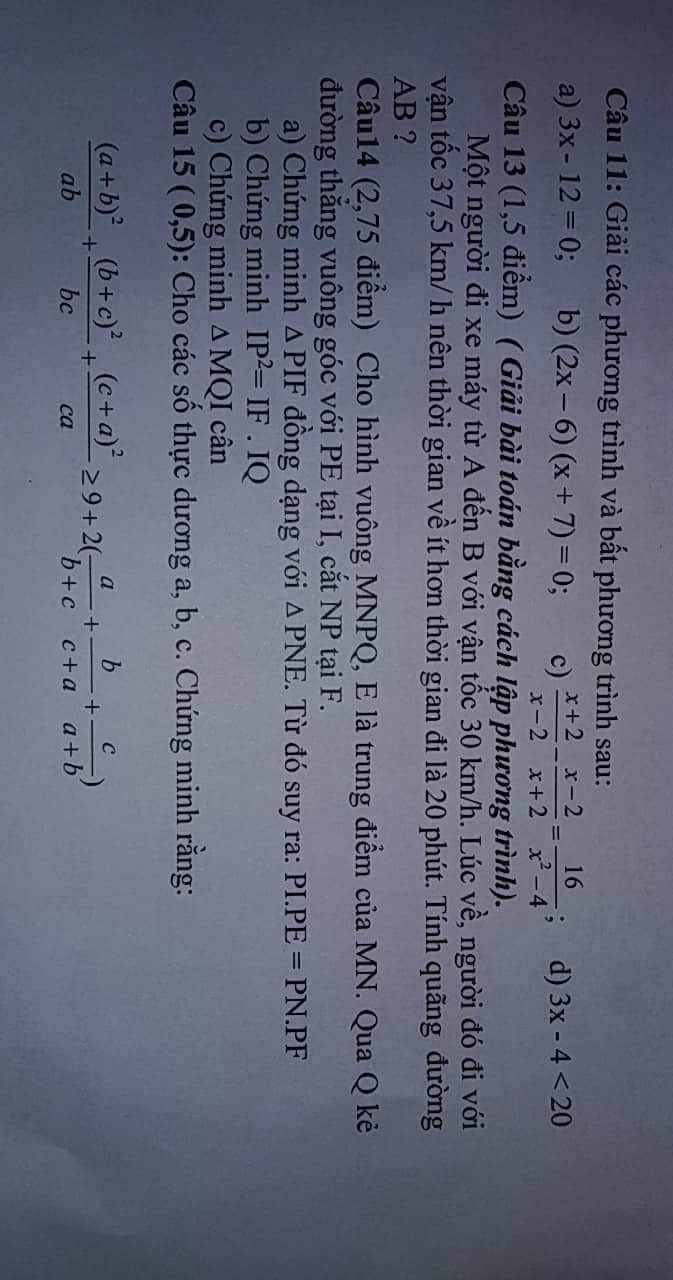
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 3:
a: \(BD=\sqrt{BC^2-DC^2}=4\left(cm\right)\)
b: \(\widehat{A}=180^0-2\cdot70^0=40^0< \widehat{B}\)
nên BC<AC=AB
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
Câu 2
a) Thay y = -2 vào biểu thức đã cho ta được:
2.(-2) + 3 = -1
Vậy giá trị của biểu thức đã cho tại y = -2 là -1
b) Thay x = -5 vào biểu thức đã cho ta được:
2.[(-5)² - 5] = 2.(25 - 5) = 2.20 = 40
Vậy giá trị của biểu thức đã cho tại x = -5 là 40


Gọi CTHH của oxit sắt cần tìm là FexOy
Khử toàn bộ oxit sắt bằng khí CO ta có phương trình sau
(1)\(Fe_xO_y+yCO\underrightarrow{t^o}xFe+yCO_2\uparrow\)
\(\Rightarrow\)Hỗn hợp khí A là CO dư và CO2.Chất rắn B là Fe
Dẫn toàn bộ khí A vào dd Ca(OH)2 ta có phương trình sau:
\(\left(2\right)CO_2+Ca\left(OH\right)_2\rightarrow CaCO_3+H_2O\)
Đặt n\(CO_2\)=a(mol) ,theo (2)\(n_{CO_2}=n_{CaCO_3}=0,12\left(mol\right)\)
Ta có:\(m_{CaCO_3}-m_{CO_2}=100a-44a=6,72\left(g\right)\)
\(\Leftrightarrow a=0,12\left(mol\right)\)
Ta lại có:\(n_{O\left(trõngoxit\right)}=n_{CO_2}=0,12\left(mol\right)\)
\(\Leftrightarrow m_{Fe}=m_{Fe_xO_y}-m_{O\left(trongoxit\right)}=6,96-0,12.16=5,04\left(g\right)\)
\(\Leftrightarrow n_{Fe}=\dfrac{5,04}{56}=0,09\left(mol\right)\)
Ta thấy \(n_{Fe}:n_O=0,09:0,12=3:4\)
\(\Rightarrow\)Oxit sắt cần tìm là Fe3O4
Cho chất rắn B và dd hỗn hơp hai muối AgNO3 và Cu(NO3)2 ta có các phương trình hóa học sau:
\(\left(3\right)Fe+2AgNO_3\rightarrow2Ag\downarrow+Fe\left(NO_3\right)_2\)
\(\left(4\right)Fe+Cu\left(NO_3\right)_2\rightarrow Cu\downarrow+Fe\left(NO_3\right)_2\)
Ta có:\(n_{AgNO_3}=1,2.0,1=0,12\left(mol\right)\)
\(n_{Cu\left(NO_3\right)_2}=0,6.0,1=0,06\left(mol\right)\)
Giả sử Fe dư trong phản ứng (3) ta có
Theo\(\left(3\right)n_{Fe\left(3\right)}=\dfrac{1}{2}n_{AgNO_3}=0,06\left(mol\right)\)<\(0,09\left(mol\right)=n_{Fe\left(có\right)}\)
\(\Rightarrow\)Giả sử đúng,\(n_{Fe\left(dư\right)}=0,09-0,06=0,03\left(mol\right)\)
Giả sử Fe hết trong phản ứng (4)
Theo(4)\(n_{Cu\left(NO_3\right)_2\left(4\right)}=n_{Fe\left(dư\right)}=0,03\left(mol\right)< 0,06\left(mol\right)=n_{Cu\left(NO_3\right)_2\left(có\right)}\)
⇒Giả sử đúng,m(g) chất rắn thu đc sau phản ứng gồm Ag và Cu
Theo(3)\(n_{Ag}=n_{AgNO_3}=0,12\left(mol\right)\)
Theo(4)\(n_{Cu}=n_{Cu\left(NO_3\right)_2\left(4\right)}=0,03\left(mol\right)\)
\(\Rightarrow m=m_{Ag}+m_{Cu}=108.0,12+64.0,03=14,88\left(g\right)\)

3. She said I should ask a lawyer.
4. Mrs Linh asked me to give Tuan this book.

Giả sử số câu trả lời đúng là x.
Theo đề bài, mỗi câu trả lời đúng được cộng 5 điểm, mỗi câu trả lời sai bị trừ 12 điểm.
Từ đó, ta có phương án:
5x - 12(30 - x) = 120
Giải phương trình trên:
5x - 360 + 12x = 120
17x = 480
x = 480/17 ≈ 28,24
Vì vậy, học sinh đã làm đúng khoảng 28 câu.
Hôm nay olm.vn sẽ hướng dẫn các em giải dạng toán nâng cao giả thiết tạm của tiểu học em nhé, cấu trúc trong đề thi chuyên và thi violympic.
Giả sử tất cả các câu trả lời là đúng thì tổng số điểm học sinh có được là:
5 \(\times\) 30 = 150 (điểm)
So với đề bài thì thừa ra là: 150 - 120 = 30 (điểm)
Cứ thay 1 câu đúng bằng 1 câu sai thì số điểm giảm là:
12 + 5 = 17 (điểm)
Số câu trả lời sai là: 30 : 17 = \(\dfrac{30}{17}\) (xem lại đề bài em nhé vì số câu không thể là lẻ)

Lề trái: cách mép trái từ 30 - 35 mm.
Lề phải: cách mép phải từ 15 - 20 mm.
Lề trên: cách mép trên từ 20 - 25 mm.
Lề dưới: cách mép dưới từ 20 - 25 mm.
lề trên: 2.54cm
lề dưới: 2.54cm
lề trái: 3.81cm
lề phải: 2.54cm
nha bạn

Refer
– Trong văn bản trên, tác giả đã đưa ra lý lẽ cho ý kiến rất thuyết phục đó là: “Ai cũng cần hoà nhập, nhưng sự hoà nhập có nhiều lối chứ không phải một. Mỗi người phải được tôn trọng, với tất cả những cái khác biệt vốn có. Sự độc đáo của từng cá nhân làm cho tập thể trở nên phong phú.”
– Như vậy, khi viết bài nghị luận cần chú ý phải đưa ra những lý lẽ và dẫn chứng thuyết phục để vấn đề nghị luận được sáng tỏ hơn.








Câu 15: (mãi mới nghĩ ra :v)
\(\dfrac{\left(a+b\right)^2}{ab}+\dfrac{\left(b+c\right)^2}{bc}+\dfrac{\left(c+a\right)^2}{ca}\ge9+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
\(\Leftrightarrow\dfrac{a^2+2ab+b^2}{ab}+\dfrac{b^2+2bc+b^2}{bc}+\dfrac{c^2+2ca+a^2}{ca}\ge9+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
\(\Leftrightarrow\dfrac{a}{b}+2+\dfrac{b}{a}+\dfrac{b}{c}+2+\dfrac{c}{b}+\dfrac{c}{a}+2+\dfrac{a}{c}\ge9+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
\(\Leftrightarrow\dfrac{a}{b}+\dfrac{b}{a}+\dfrac{b}{c}+\dfrac{c}{b}+\dfrac{c}{a}+\dfrac{a}{c}\ge3+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
\(\Leftrightarrow a\left(\dfrac{1}{b}+\dfrac{1}{c}\right)+b\left(\dfrac{1}{c}+\dfrac{1}{a}\right)+c\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\ge3+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
-Áp dụng BĐT Caushy Schwarz ta có:
\(\left\{{}\begin{matrix}\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{\left(1+1\right)^2}{b+c}=\dfrac{4}{b+c}\\\dfrac{1}{c}+\dfrac{1}{a}\ge\dfrac{\left(1+1\right)^2}{c+a}=\dfrac{4}{c+a}\\\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{\left(1+1\right)^2}{a+b}=\dfrac{4}{a+b}\end{matrix}\right.\)
-Từ đó suy ra: \(a\left(\dfrac{1}{b}+\dfrac{1}{c}\right)+b\left(\dfrac{1}{c}+\dfrac{1}{a}\right)+c\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\ge\dfrac{4a}{b+c}+\dfrac{4b}{c+a}+\dfrac{4c}{a+b}\)
-Ta c/m rằng: \(\dfrac{4a}{b+c}+\dfrac{4b}{c+a}+\dfrac{4c}{a+b}\ge3+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
\(\Leftrightarrow2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\ge3+2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\)
\(\Leftrightarrow2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)\ge3\)
\(\Leftrightarrow2\left(\dfrac{a}{b+c}+1+\dfrac{b}{c+a}+1+\dfrac{c}{a+b}+1-3\right)\ge3\)
\(\Leftrightarrow2\left(\dfrac{a+b+c}{b+c}+\dfrac{b+c+a}{c+a}+\dfrac{c+a+b}{a+b}\right)-6\ge3\)
\(\Leftrightarrow2\left(a+b+c\right)\left(\dfrac{1}{b+c}+\dfrac{1}{c+a}+\dfrac{1}{a+b}\right)\ge9\left(1\right)\)
-Áp dụng BĐT Caushy Schwarz cho VT của BĐT ta được:
\(2\left(a+b+c\right)\left(\dfrac{1}{b+c}+\dfrac{1}{c+a}+\dfrac{1}{a+b}\right)\ge2\left(a+b+c\right)\left(\dfrac{\left(1+1+1\right)^2}{a+b+b+c+c+a}\right)=2\left(a+b+c\right)\dfrac{9}{2\left(a+b+c\right)}=9\)
\(\Rightarrow\)BĐT (1) đúng.
\(\Rightarrowđpcm\)
-Dấu "=" xảy ra khi \(a=b=c\)