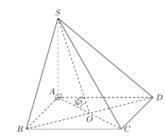
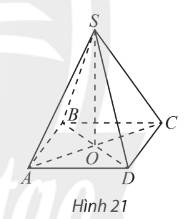
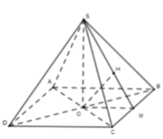
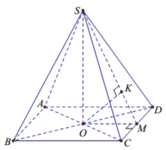
Cho hình chóp S.ABCD có đáy là hình vuông tâm O , cạnh a ; các cạnh bên của hình chóp cùng bằng
a. Chứng minh rằng đường thẳng BD vuông góc với (SAC)
b. Gọi P là mặt phẳng đi qua A và vuông góc với đường thẳng SC. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (P)
c. Tính góc giữa mặt phẳng (P) và đường thẳng AB




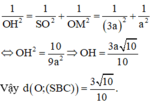
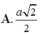
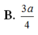
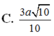
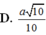



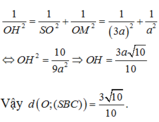
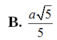

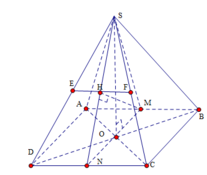
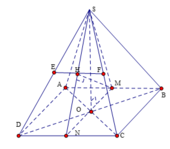
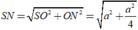
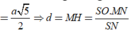
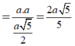
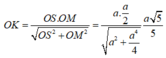
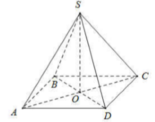
a: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
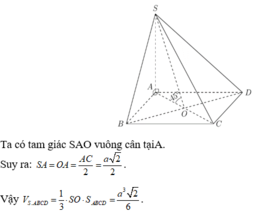
b: Tham khảo: