a) Giải hệ phương trình
2x+2y=7
2x-2y=3
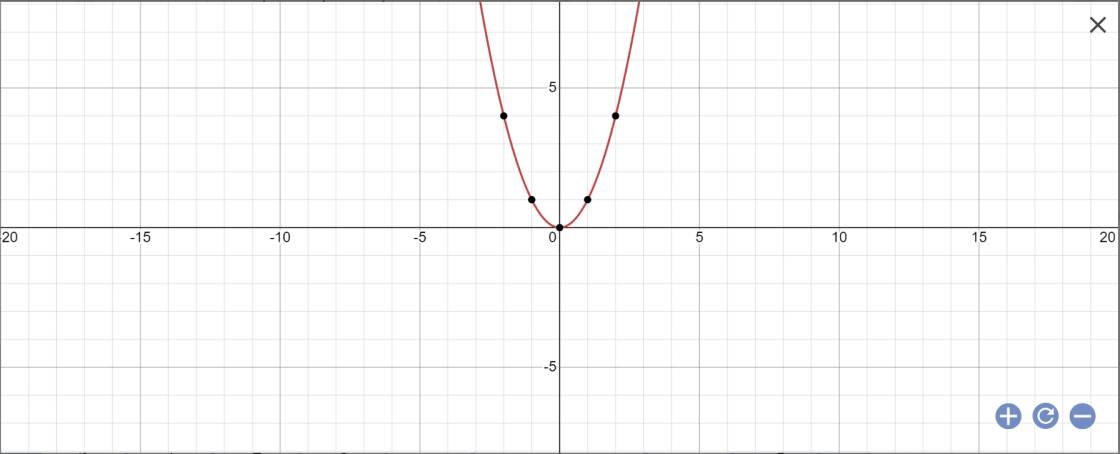
b) Cho hàm số y = x2 có đồ thị là parabol (p). Vẽ parabol (p) trên mặt phẳng tọa độ Oxy.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Ta có: \(y'=\left(x^2\right)'=2x\Rightarrow y'\left(1\right)=2\cdot1=2\)
Vậy hệ số góc của tiếp tuyến của parabol \(y=x^2\) tại điểm có hoàng độà k = 2.
b, Ta có: \(y_0=1^2=1\)
Vậy phương trình tiếp tuyến là \(y=y'\left(x_0\right)\left(x-x_0\right)+y_0=2\left(x-1\right)+1=2x-1\)

Bài 5:
a: Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
=>AD\(\perp\)DB tại D
=>AD\(\perp\)BC tại D
Xét ΔABC vuông tại A có AD là đường cao
nên \(AC^2=CD\cdot CB\)
b: Ta có: ΔOAE cân tại O
mà OC là đường cao
nên OC là phân giác của góc AOE
Xét ΔOAC và ΔOEC có
OA=OE
\(\widehat{AOC}=\widehat{EOC}\)
OC chung
Do đó: ΔOAC=ΔOEC
=>\(\widehat{OAC}=\widehat{OEC}\)
mà \(\widehat{OAC}=90^0\)
nên \(\widehat{OEC}=90^0\)
=>CE là tiếp tuyến của (O)
Bài 3:
a: 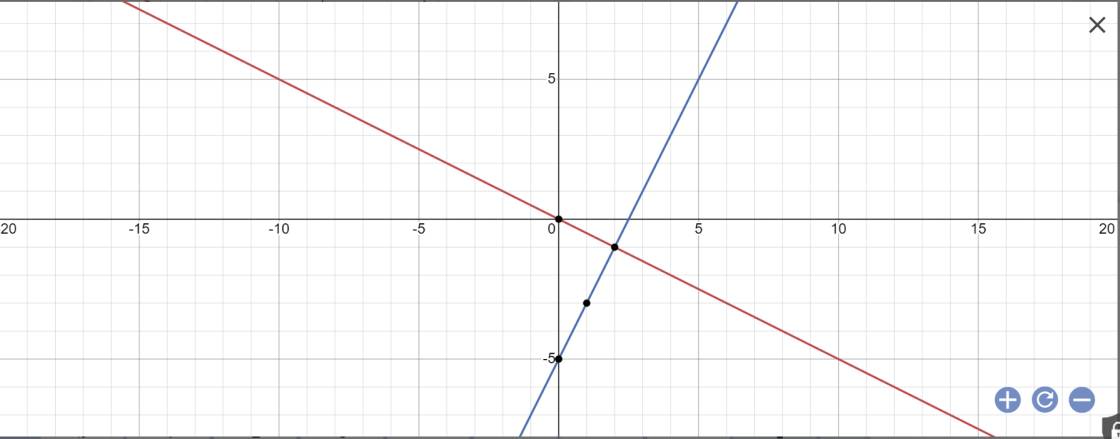
b: Phương trình hoành độ giao điểm là:
\(-\dfrac{1}{2}x=2x-5\)
=>\(-\dfrac{1}{2}x-2x=-5\)
=>\(-\dfrac{5}{2}x=-5\)
=>x=2
Thay x=2 vào y=-1/2x, ta được:
\(y=-\dfrac{1}{2}\cdot2=-1\)
Vậy: (d) cắt (d') tại điểm A(2;-1)
a: =>4x=10 và x-y=3/2
=>x=5/2 và y=1
b: