cho số thập phân vô hạn tuần hoàn a=1,020202...9(chu kì là 02).hãy viết a dưới dạng một phân số
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: a= 1,02020202... ( chu kì 2)
= 1 + 0,02+ 0,0002+ 0,000002 + .....

Là tổng của cấp số nhân lùi vô hạn có số hạng đầu là
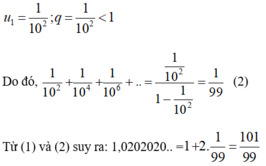

\(a=34,\left(12\right)\)
\(=34\dfrac{12}{99}=34\dfrac{4}{33}=\dfrac{1126}{33}\)

Ta có: \(\frac{1}{4} = 0,25\). Đây là số thập phân hữu hạn.
\( - \frac{2}{{11}} = - 0,1818....\). Đây là số thập phân vô hạn tuần hoàn. Chu kì của nó là 18. Ta viết \( - \frac{2}{{11}}=-0,(18)\)

Phân số hữu hạn là : \(\frac{5}{8}=0.625,-\frac{3}{20}=-0.15\)\(\frac{14}{35}=\frac{2}{5}=0.4\) vì mẫu tối giản của chúng là tích của các lũy thừa 2 và 5.
Phân số còn lại là vô hạn tuần hoàn vì mẫu của chúng không phân tích được thành tích của các lúy thừa 2 và 5.
Số \(\frac{4}{11}=0.\left(36\right),\frac{15}{22}=0.68\left(18\right),-\frac{7}{12}=-0.58\left(3\right)\)

2,131131131...
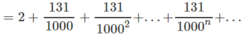
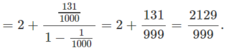
(Vì 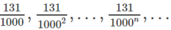
là một cấp số nhân lùi vô hạn với công bội 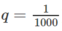 )
)

a) - Viết dạng thập phân vô hạn tuần hoàn:\(\dfrac{1}{9};\dfrac{1}{99}\) là: \(\dfrac{1}{9}=0,(1);\dfrac{1}{99}=0,(01)\)
- Nhận xét:
Dạng thập phân vô hạn tuần hoàn của phân số có dạng \(\dfrac{1}{99...9}\) như sau:
\(\dfrac{1}{99...9}= 0,(0…001) \) ( n chữ số 9); ( \(n-1\) chữ số 0)
b) Dự đoán kết quả của \(\dfrac{1}{999}\)
Theo nhận xét ở câu a ta có: \(\dfrac{1}{999}=0,(001)\)
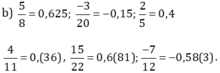
ai trả lời đầu tiên mình k cho